Source: Principles of Physics
Problem Sets:
Problem
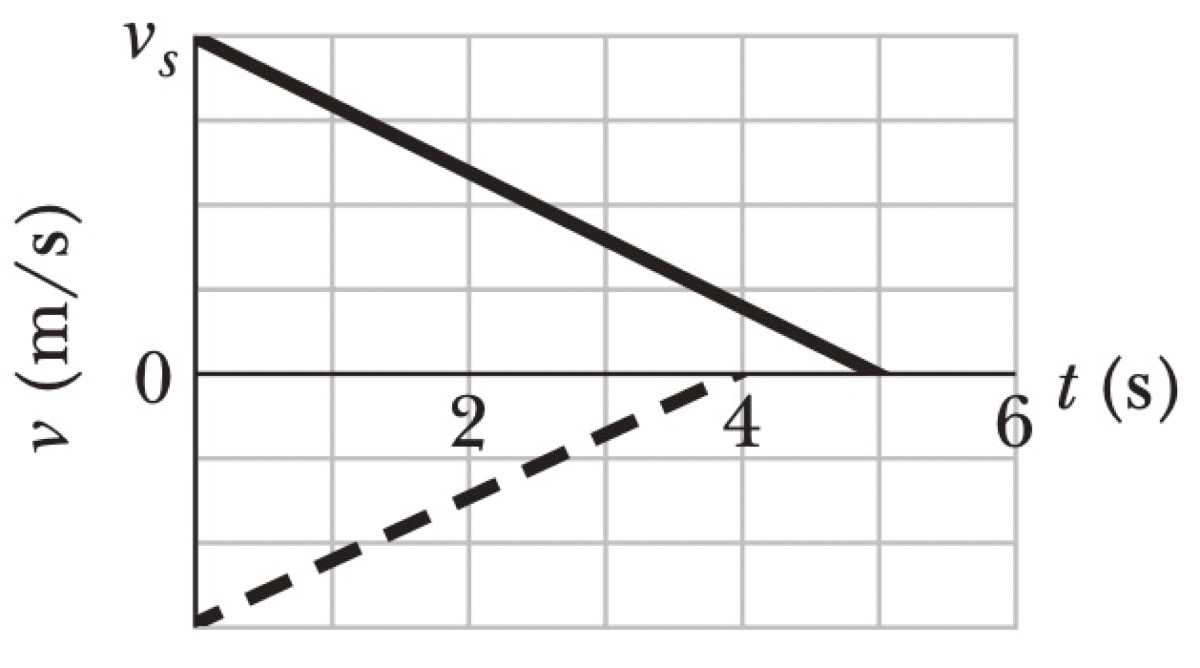
Two trains are moving along the same track and are headed toward each other. Their conductors simultaneously apply the brakes. The velocity-time graph in Figure shows their velocities $v$ as a function of time $t$ during the slowing process. The vertical scaling of the graph is set by $v_s = 40.0$ m/s. The braking process begins when the trains are 200 m apart.
The final separation between the trains is given by:
$$d_{final} = d_{initial} - \left( \frac{1}{2} t_1 |v_{1,i}| + \frac{1}{2} t_2 |v_{2,i}| \right)$$Substituting the values from the problem and the graph:
$$d_{final} = 200 \text{ m} - \left( \frac{1}{2} (5.0 \text{ s})(40.0 \text{ m/s}) + \frac{1}{2} (4.0 \text{ s})(30.0 \text{ m/s}) \right)$$ $$d_{final} = 200 \text{ m} - (100 \text{ m} + 60 \text{ m})$$ $$d_{final} = 40 \text{ m}$$The final separation of the two trains is the initial separation minus the total distance traveled by both trains toward each other. The distance traveled by each train can be found from the area under its velocity-time graph.
Let the train with the initial positive velocity be Train 1 (solid line) and the train with the initial negative velocity be Train 2 (dashed line). Their motions are independent until they potentially collide. We need to find the distance each travels before stopping.
From the graph, we extract the initial velocities and stopping times:
- Train 1: Initial velocity $v_{1,i} = v_s = 40.0$ m/s. It stops at time $t_1 = 5.0$ s.
- Train 2: The vertical scale is $v_s = 40.0$ m/s over 4 divisions, so each division is 10.0 m/s. The initial velocity is at -3 divisions, so $v_{2,i} = -30.0$ m/s. It stops at time $t_2 = 4.0$ s.
The displacement of an object is the area under its $v-t$ graph. For constant acceleration (a straight line on the $v-t$ graph), this area is a triangle. The distance traveled is the magnitude of the displacement.
For Train 1, the distance traveled $d_1$ is the area of the triangle formed by its graph:
$$d_1 = |\Delta x_1| = \left| \frac{1}{2} \times \text{base} \times \text{height} \right| = \frac{1}{2} t_1 |v_{1,i}|$$For Train 2, the distance traveled $d_2$ is the area of the triangle below the time axis:
$$d_2 = |\Delta x_2| = \frac{1}{2} t_2 |v_{2,i}|$$The total distance covered by both trains, which reduces their initial separation, is $d_{total} = d_1 + d_2$. The final separation $d_{final}$ is the initial separation $d_{initial}$ minus this total distance.
$$d_{final} = d_{initial} - d_{total} = d_{initial} - (d_1 + d_2)$$ $$d_{final} = d_{initial} - \left( \frac{1}{2} t_1 |v_{1,i}| + \frac{1}{2} t_2 |v_{2,i}| \right)$$Substituting the numerical values:
$$d_1 = \frac{1}{2} (5.0 \text{ s})(40.0 \text{ m/s}) = 100 \text{ m}$$ $$d_2 = \frac{1}{2} (4.0 \text{ s})(30.0 \text{ m/s}) = 60 \text{ m}$$ $$d_{total} = 100 \text{ m} + 60 \text{ m} = 160 \text{ m}$$Given the initial separation $d_{initial} = 200$ m:
$$d_{final} = 200 \text{ m} - 160 \text{ m} = 40 \text{ m}$$Since the total distance traveled (160 m) is less than the initial separation (200 m), the trains do not collide.
Alternative (Calculus-based derivation): The acceleration is the slope of the v-t graph, $a = dv/dt$.
$a_1 = (0 - 40.0)/(5.0 - 0) = -8.0 \text{ m/s}^2$ $a_2 = (0 - (-30.0))/(4.0 - 0) = 7.5 \text{ m/s}^2$The distance is the integral of the magnitude of velocity:
$d_1 = \int_0^{t_1} v_1(t) dt = \int_0^{5.0} (40.0 - 8.0t) dt = [40.0t - 4.0t^2]_0^{5.0} = 200 - 100 = 100$ m $d_2 = \int_0^{t_2} |v_2(t)| dt = \int_0^{4.0} |-30.0 + 7.5t| dt = \int_0^{4.0} (30.0 - 7.5t) dt = [30.0t - 3.75t^2]_0^{4.0} = 120 - 60 = 60$ mThe final separation is $d_{final} = 200 \text{ m} - (100 \text{ m} + 60 \text{ m}) = 40 \text{ m}$, confirming the result.