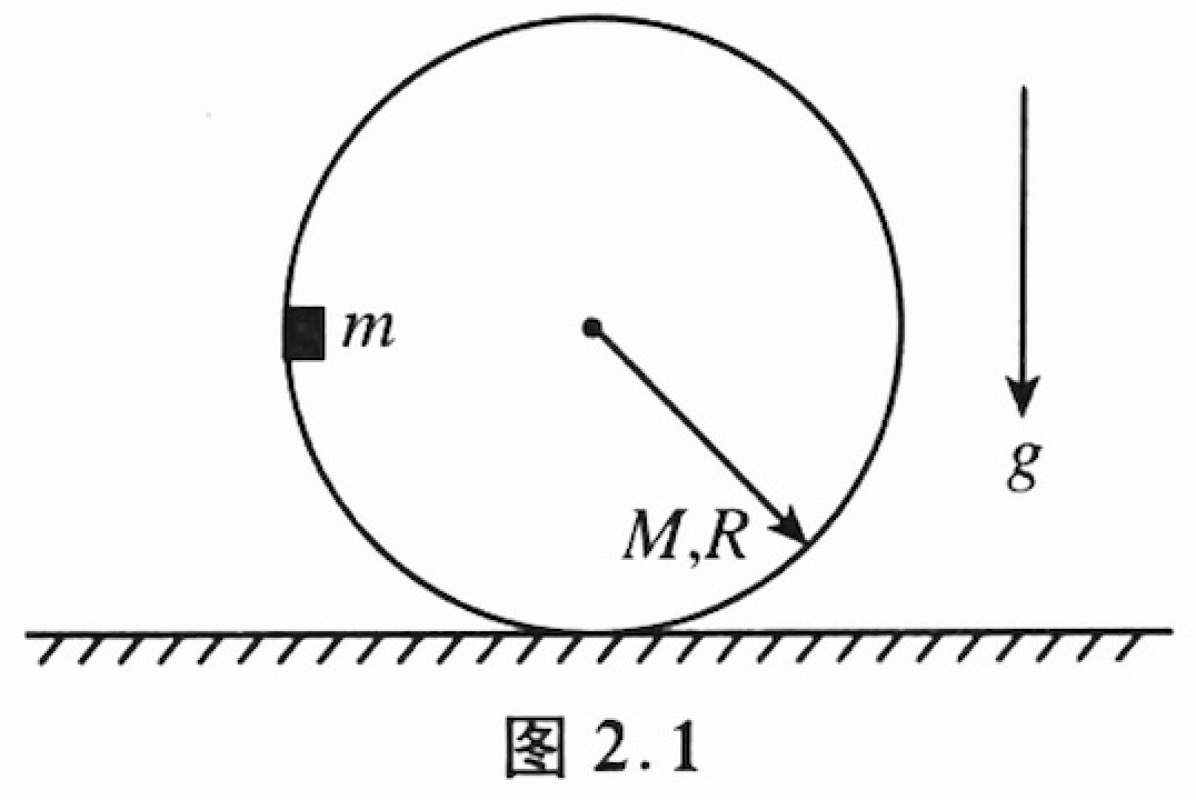
This problem can be solved by applying the principles of conservation of energy and analyzing the equations of motion for the block and the cylinder. Let's denote the horizontal velocity of the block relative to the ground as $v_b$ and the horizontal velocity of the cylinder's center of mass as $V_c$ when the block reaches the lowest point.

Step 1: Derive the relationship between velocities Let's analyze the horizontal forces acting on the block and the cylinder. Let $N_x$ be the horizontal component of the normal force from the cylinder on the block. By Newton's third law, the block exerts a force $-N_x$ on the cylinder. Let $f$ be the static friction force exerted by the ground on the cylinder.

For the block, Newton's second law in the horizontal direction is:

$$ N_x = m a_b $$

where $a_b$ is the horizontal acceleration of the block.

For the cylinder, the translational equation of motion in the horizontal direction is:

$$ -N_x + f = M a_c $$

where $a_c$ is the acceleration of the cylinder's center of mass. The torque about the center of mass is provided by the friction force:

$$ \tau = f R = I \alpha $$

For a hollow cylinder, the moment of inertia is $I = MR^2$. For rolling without slipping, the angular acceleration is $\alpha = a_c/R$.

$$ f R = (MR^2) \frac{a_c}{R} \implies f = M a_c $$

Substitute $f$ back into the translational equation for the cylinder:

$$ -N_x + M a_c = M a_c \implies -N_x = 0 $$

This seems incorrect. Let's reconsider the force from the block. The force from the block is $N_b$, which is always normal to the surface. Let's use the horizontal component $N_{bx}$. The force on the cylinder is the reaction force from the block, which is $N_{bx}$ in the forward direction (assuming the block is sliding down to the right).

$$ N_{bx} - f = M a_c $$

And for the block, the force from the cylinder is $-N_{bx}$:

$$ -N_{bx} = m a_{b,x} $$

Combining these with $f = M a_c$:

$$ N_{bx} - M a_c = M a_c \implies N_{bx} = 2 M a_c $$

Now substitute this into the block's equation:

$$ -(2 M a_c) = m a_{b,x} \implies m a_{b,x} + 2 M a_c = 0 $$

Since both objects start from rest, we can integrate this relationship with respect to time to get the relationship between their final horizontal velocities:

$$ m v_b + 2 M V_c = 0 \quad \text{(Equation 1)} $$

Step 2: Apply Conservation of Mechanical Energy The system consists of the block and the cylinder. The static friction force does no work, and the normal forces are internal or do no work. Gravity is a conservative force. Therefore, the total mechanical energy of the system is conserved. Initial energy ($E_i$): The block is at height $R$ and at rest. The cylinder is at rest.

$$ E_i = mgR $$

Final energy ($E_f$): The block is at the bottom (height 0) with velocity $v_b$. The cylinder's center has velocity $V_c$ and it's rolling. The kinetic energy of the rolling hollow cylinder is the sum of its translational and rotational kinetic energy:

$$ K_c = \frac{1}{2} M V_c^2 + \frac{1}{2} I \omega^2 = \frac{1}{2} M V_c^2 + \frac{1}{2} (MR^2) \left(\frac{V_c}{R}\right)^2 = M V_c^2 $$

The kinetic energy of the block is $K_b = \frac{1}{2} m v_b^2$. So, the total final energy is:

$$ E_f = \frac{1}{2} m v_b^2 + M V_c^2 $$

By conservation of energy, $E_i = E_f$:

$$ mgR = \frac{1}{2} m v_b^2 + M V_c^2 \quad \text{(Equation 2)} $$

Step 3: Solve for the velocities From Equation 1, we express $V_c$ in terms of $v_b$:

$$ V_c = -\frac{m v_b}{2M} $$

Substitute this into Equation 2:

$$ mgR = \frac{1}{2} m v_b^2 + M \left(-\frac{m v_b}{2M}\right)^2 $$ $$ mgR = \frac{1}{2} m v_b^2 + M \frac{m^2 v_b^2}{4M^2} = \left(\frac{m}{2} + \frac{m^2}{4M}\right) v_b^2 $$ $$ mgR = m \left(\frac{1}{2} + \frac{m}{4M}\right) v_b^2 = m \left(\frac{2M+m}{4M}\right) v_b^2 $$

Solving for $v_b^2$:

$$ v_b^2 = \frac{4M g R}{2M+m} $$

Step 4: Calculate the Interaction Force At the lowest point, we analyze the forces on the block in the vertical direction. The net force provides the centripetal acceleration. The interaction force $F$ acts upwards, and gravity $mg$ acts downwards.

$$ F - mg = m a_{y} $$

The acceleration $a_y$ is the centripetal acceleration of the block relative to the center of the cylinder, as the cylinder's center has no vertical acceleration. This acceleration depends on the relative speed, $v_{rel}$, between the block and the cylinder's center.

$$ a_y = \frac{v_{rel}^2}{R} $$

The relative speed at the bottom is:

$$ v_{rel} = v_b - V_c = v_b - \left(-\frac{m v_b}{2M}\right) = v_b \left(1 + \frac{m}{2M}\right) = v_b \left(\frac{2M+m}{2M}\right) $$

Now we find $v_{rel}^2$:

$$ v_{rel}^2 = v_b^2 \left(\frac{2M+m}{2M}\right)^2 = \left(\frac{4M g R}{2M+m}\right) \frac{(2M+m)^2}{4M^2} = \frac{gR(2M+m)}{M} $$

Substitute this into the force equation:

$$ F - mg = m \frac{v_{rel}^2}{R} = m \frac{1}{R} \left(\frac{gR(2M+m)}{M}\right) = mg \frac{2M+m}{M} $$

Finally, solve for the interaction force $F$:

$$ F = mg + mg \frac{2M+m}{M} = mg \left(1 + \frac{2M+m}{M}\right) = mg \left(\frac{M+2M+m}{M}\right) $$ $$ F = mg \frac{3M+m}{M} $$