Source: Collection of Difficult Physics Problems
Problem Sets:
Problem
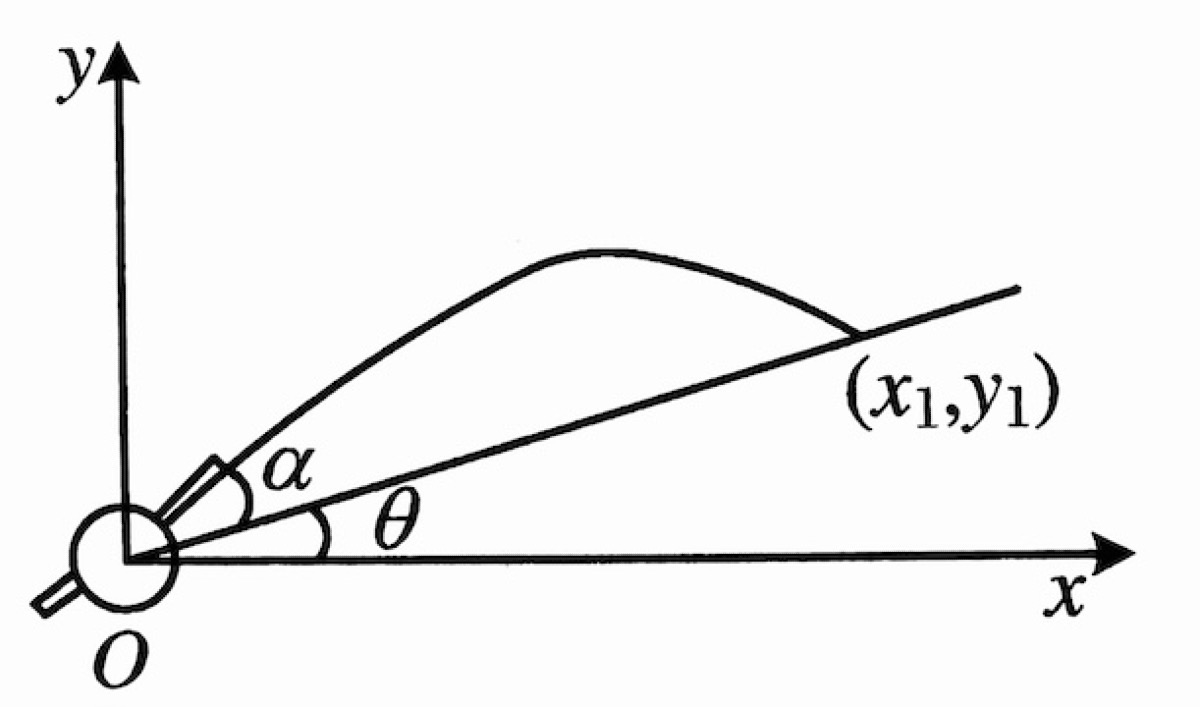
As shown in Figure, a cannon is situated on a hillside plane with an inclination angle of $\theta$. The cannon fires a projectile with an initial velocity of $v_0$ at an elevation angle of $\alpha$ relative to the slope. Air resistance is to be neglected.
- Find the position where the projectile lands on the slope.
- Find the elevation angle $\alpha$ that achieves the maximum range along the slope.
[A1] The projectile lands at the position $(x_1, y_1)$ given by:
$$x_1 = \frac{2 v_0^2 \sin\alpha \cos(\alpha+\theta)}{g \cos\theta}$$ $$y_1 = \frac{2 v_0^2 \sin\alpha \cos(\alpha+\theta) \sin\theta}{g \cos^2\theta}$$The range along the slope is $R = \sqrt{x_1^2+y_1^2} = \frac{2 v_0^2 \sin\alpha \cos(\alpha+\theta)}{g \cos^2\theta}$.
[A2] The elevation angle $\alpha$ that achieves the maximum range along the slope is:
$$\alpha = \frac{\pi}{4} - \frac{\theta}{2}$$To solve this problem, we use a coordinate system $(x', y')$ tilted at an angle $\theta$ with respect to the horizontal. The $x'$-axis lies along the inclined plane, and the $y'$-axis is perpendicular to it.
In this tilted frame, the acceleration due to gravity, $\vec{g}$, has components:
$$g_{x'} = -g \sin\theta$$ $$g_{y'} = -g \cos\theta$$The initial velocity, $v_0$, at an angle $\alpha$ relative to the slope, has components:
$$v_{0x'} = v_0 \cos\alpha$$ $$v_{0y'} = v_0 \sin\alpha$$The equations for the projectile's position are:
$$y'(t) = v_{0y'}t + \frac{1}{2}g_{y'}t^2 = (v_0 \sin\alpha)t - \frac{1}{2}(g \cos\theta)t^2$$ $$x'(t) = v_{0x'}t + \frac{1}{2}g_{x'}t^2 = (v_0 \cos\alpha)t - \frac{1}{2}(g \sin\theta)t^2$$The projectile lands on the slope when $y'(T) = 0$ for a time of flight $T > 0$.
$$(v_0 \sin\alpha)T - \frac{1}{2}(g \cos\theta)T^2 = 0$$Solving for $T$:
$$T = \frac{2 v_0 \sin\alpha}{g \cos\theta}$$[Q1] Find the position where the projectile lands on the slope.
The range $R$ along the slope is the distance $x'(T)$ traveled in the $x'$-direction during the flight time $T$.
$$R = x'(T) = (v_0 \cos\alpha)T - \frac{1}{2}(g \sin\theta)T^2$$Substituting the expression for $T$:
$$R = v_0 \cos\alpha \left(\frac{2 v_0 \sin\alpha}{g \cos\theta}\right) - \frac{1}{2} g \sin\theta \left(\frac{2 v_0 \sin\alpha}{g \cos\theta}\right)^2$$ $$R = \frac{2 v_0^2}{g \cos^2\theta} (\sin\alpha \cos\alpha \cos\theta - \sin^2\alpha \sin\theta)$$ $$R = \frac{2 v_0^2 \sin\alpha}{g \cos^2\theta} (\cos\alpha \cos\theta - \sin\alpha \sin\theta)$$Using the trigonometric identity $\cos(\alpha+\theta) = \cos\alpha\cos\theta - \sin\alpha\sin\theta$:
$$R = \frac{2 v_0^2 \sin\alpha \cos(\alpha+\theta)}{g \cos^2\theta}$$The landing position $(x_1, y_1)$ in the original horizontal-vertical coordinate system is found by converting the range $R$ back to these coordinates:
$$x_1 = R \cos\theta = \frac{2 v_0^2 \sin\alpha \cos(\alpha+\theta)}{g \cos\theta}$$ $$y_1 = R \sin\theta = \frac{2 v_0^2 \sin\alpha \cos(\alpha+\theta) \sin\theta}{g \cos^2\theta}$$[Q2] Find the elevation angle $\alpha$ that achieves the maximum range along the slope.
To maximize the range $R$, we need to maximize the part of the expression that depends on $\alpha$: $f(\alpha) = \sin\alpha \cos(\alpha+\theta)$. We use the product-to-sum trigonometric identity $2 \sin A \cos B = \sin(A+B) + \sin(A-B)$.
$$2 \sin\alpha \cos(\alpha+\theta) = \sin(\alpha + (\alpha+\theta)) + \sin(\alpha - (\alpha+\theta))$$ $$= \sin(2\alpha+\theta) + \sin(-\theta) = \sin(2\alpha+\theta) - \sin\theta$$So the range can be written as:
$$R(\alpha) = \frac{v_0^2}{g \cos^2\theta} [\sin(2\alpha+\theta) - \sin\theta]$$To maximize $R(\alpha)$ for a fixed $\theta$, we must maximize the term $\sin(2\alpha+\theta)$. The maximum value of the sine function is 1, which occurs when its argument is $\pi/2$.
$$\sin(2\alpha+\theta) = 1$$ $$2\alpha+\theta = \frac{\pi}{2}$$Solving for the optimal angle $\alpha$:
$$\alpha = \frac{\pi}{4} - \frac{\theta}{2}$$