Source: Collection of Difficult Physics Problems
Problem
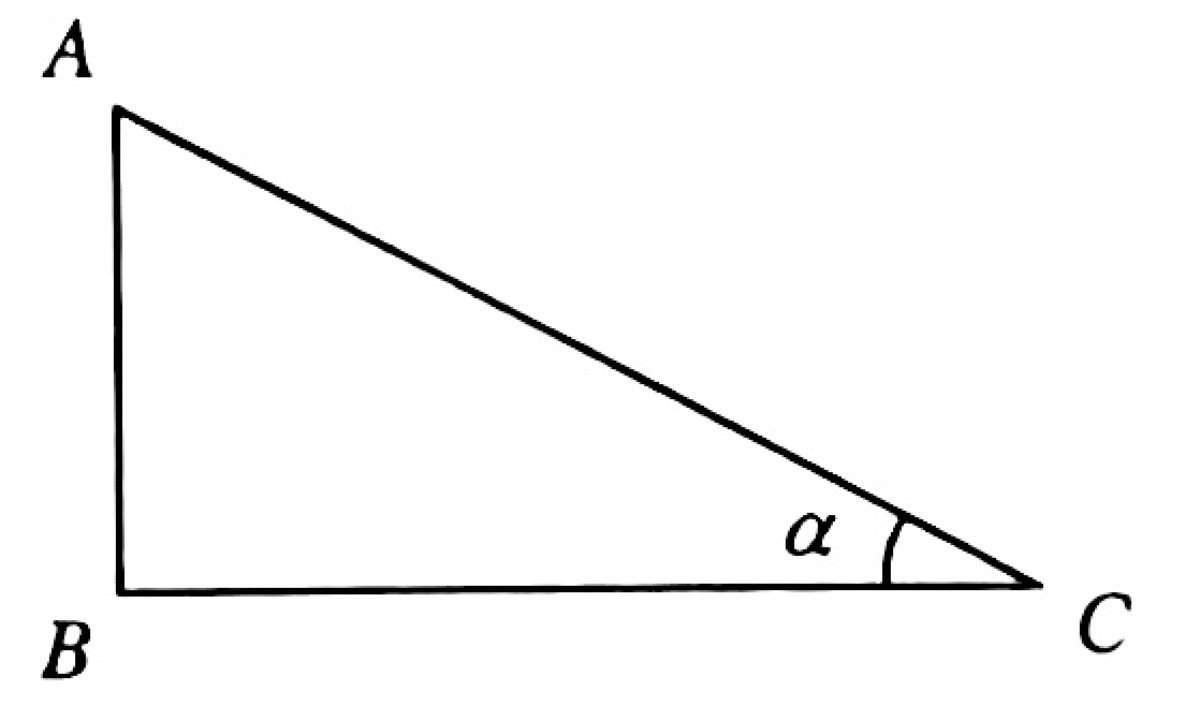
As shown in the figure, a right-angled triangle ABC is situated in a vertical plane, with side BC being horizontal and side AB being vertical. The angle between the hypotenuse AC and the horizontal side BC is $\alpha$. A point mass starts from rest at point A and travels to point C under the influence of gravity, constrained to move along specified paths.
Path 1 involves the particle moving along the sides AB and then BC. The time taken for the segment AB is $t_1$, and the time for the segment BC is $t_2$. Path 2 involves the particle moving along the hypotenuse AC. The time taken is $t_3$.
It is assumed that the particle turns at corner B instantaneously and that the magnitude of its velocity is conserved during the turn. The paths are smooth, so there is no friction.
- Find the value of angle $\alpha$ for which the total time taken for both paths is equal, i.e., $t_1 + t_2 = t_3$.
- For the value of $\alpha$ found in Q1, consider all possible paths from A to C within the triangle that consist only of vertical and horizontal segments. Which of these paths takes the most time to travel?
- Which of these paths takes the least time?
- What is the ratio of the longest possible time to the shortest possible time?
[Q1] The value of the angle is $\alpha = \arcsin(3/5)$. [Q2] The path that takes the most time is the one composed of infinitesimal stairsteps that follows the hypotenuse AC. [Q3] The path that takes the least time is along the sides AB and then BC. [Q4] The ratio of the longest possible time to the shortest possible time is $7/5$.
Let the height of the triangle be $h=|AB|$ and the base be $b=|BC|$. The hypotenuse is $L=|AC|$. From trigonometry, we have $h = b \tan \alpha$ and $L = h / \sin \alpha$. The acceleration due to gravity is $g$.
[Q1] Find $\alpha$ such that $t_1+t_2=t_3$.
Path 1 (A → B → C):
-
Motion along AB (vertical drop): The particle starts from rest and falls a distance $h$ under acceleration $g$. Using $s = \frac{1}{2}at^2$, the time $t_1$ is:
$$h = \frac{1}{2}gt_1^2 \implies t_1 = \sqrt{\frac{2h}{g}}$$The speed at B is $v_B = gt_1 = \sqrt{2gh}$.
-
Motion along BC (horizontal): The speed is constant at $v_B$ since magnitude of velocity is conserved at the turn. The distance is $b$. The time $t_2$ is:
$$t_2 = \frac{b}{v_B} = \frac{b}{\sqrt{2gh}}$$The total time for Path 1 is $T_{ABC} = t_1 + t_2 = \sqrt{\frac{2h}{g}} + \frac{b}{\sqrt{2gh}}$.
Path 2 (A → C):
- Motion along AC (inclined plane): The particle starts from rest and moves a distance $L = h/\sin\alpha$. The acceleration along the incline is $a_{AC} = g \sin\alpha$. Using $s = \frac{1}{2}at^2$, the time $t_3$ is: $$\frac{h}{\sin\alpha} = \frac{1}{2}(g\sin\alpha)t_3^2 \implies t_3 = \frac{1}{\sin\alpha}\sqrt{\frac{2h}{g}}$$
Equating the times: Set $t_1+t_2 = t_3$:
$$\sqrt{\frac{2h}{g}} + \frac{b}{\sqrt{2gh}} = \frac{1}{\sin\alpha}\sqrt{\frac{2h}{g}}$$Dividing by $\sqrt{2h/g}$:
$$1 + \frac{b}{2h} = \frac{1}{\sin\alpha}$$Using the geometric relation $b/h = \cot\alpha$:
$$1 + \frac{\cot\alpha}{2} = \frac{1}{\sin\alpha} \implies 2\sin\alpha + \cos\alpha = 2$$To solve this, let $s=\sin\alpha$ and $c=\cos\alpha$. With $c = 2-2s$ and $s^2+c^2=1$:
$$s^2 + (2-2s)^2 = 1 \implies 5s^2 - 8s + 3 = 0$$Factoring gives $(5s-3)(s-1)=0$. The solutions are $s=1$ (for $\alpha=90^\circ$, a trivial case) and $s=3/5$. The non-trivial solution is $\sin\alpha = 3/5$. For this solution, $\cos\alpha = \sqrt{1-(3/5)^2}=4/5$, and $\tan\alpha = 3/4$.
[Q2] & [Q3] Longest and shortest time for stairstep paths.
Consider a general path from A to C consisting of vertical and horizontal segments. Let the path consist of $N$ steps, with the $i$-th step involving a vertical drop $\Delta h_i$ followed by a horizontal segment $\Delta b_i$. The total time is $T = T_{vert} + T_{horiz}$.
The total time for all vertical segments, $T_{vert}$, can be shown to be constant regardless of the path. Let $v_{i-1}$ be the speed at the start of the $i$-th vertical drop. The time for this drop is $\Delta t_{v,i} = (v_i - v_{i-1})/g$, where $v_i = \sqrt{v_{i-1}^2 + 2g\Delta h_i}$. The total vertical time is a telescoping sum:
$$T_{vert} = \sum_{i=1}^{N} \Delta t_{v,i} = \frac{1}{g} \sum_{i=1}^{N} (v_i - v_{i-1}) = \frac{v_N - v_0}{g} = \frac{\sqrt{2gh} - 0}{g} = \sqrt{\frac{2h}{g}}$$This is simply $t_1$.
The total time for horizontal segments is $T_{horiz} = \sum_{i=1}^{N} \frac{\Delta b_i}{v_i}$, where $v_i = \sqrt{2g\sum_{j=1}^i \Delta h_j}$ is the constant speed during the $i$-th horizontal segment. The total time for any stairstep path is:
$$T = \sqrt{\frac{2h}{g}} + \sum_{i=1}^{N} \frac{\Delta b_i}{v_i}$$To extremize $T$, we must extremize $T_{horiz}$.
Shortest Time (Q3):
$T_{horiz}$ is minimized when the speeds $v_i$ are maximized for each segment $\Delta b_i$. This occurs when all the vertical drop happens first, maximizing the speed for all subsequent horizontal travel. This corresponds to the path A→B→C. $$T_{shortest} = T_{ABC} = \sqrt{\frac{2h}{g}} + \frac{b}{\sqrt{2gh}}$$Longest Time (Q2):
$T_{horiz}$ is maximized when the speeds $v_i$ are minimized for each segment $\Delta b_i$. This is achieved by performing horizontal travel as early as possible, when the accumulated drop is small. This corresponds to a path of infinitesimal steps that hugs the hypotenuse AC. For such a path, the total time for horizontal segments can be found by integrating: $$T_{horiz, max} = \int_0^b \frac{dx}{v(x)}$$where $v(x) = \sqrt{2gy(x)}$ and $y(x)=x\tan\alpha$ is the height dropped.
$v(x) = \sqrt{2gx\tan\alpha}$. $$T_{horiz, max} = \int_0^b \frac{dx}{\sqrt{2gx\tan\alpha}} = \frac{1}{\sqrt{2g\tan\alpha}} [2\sqrt{x}]_0^b = \sqrt{\frac{2b}{g\tan\alpha}}$$ $$T_{longest} = \sqrt{\frac{2h}{g}} + \sqrt{\frac{2b}{g\tan\alpha}}$$[Q4] Ratio of longest to shortest time.
Using the value of $\alpha$ from Q1 where $\sin\alpha=3/5$ and $\tan\alpha=3/4$, we have $\cot\alpha = 4/3$. We express the times in terms of $h$ and $\alpha$.
$$T_{shortest} = \sqrt{\frac{2h}{g}} \left(1 + \frac{b}{2h}\right) = \sqrt{\frac{2h}{g}} \left(1 + \frac{\cot\alpha}{2}\right)$$ $$T_{longest} = \sqrt{\frac{2h}{g}} + \sqrt{\frac{2(h\cot\alpha)}{g\tan\alpha}} = \sqrt{\frac{2h}{g}} (1 + \sqrt{\cot^2\alpha}) = \sqrt{\frac{2h}{g}} (1 + \cot\alpha)$$The ratio is:
$$\frac{T_{longest}}{T_{shortest}} = \frac{1 + \cot\alpha}{1 + \frac{1}{2}\cot\alpha}$$Substituting $\cot\alpha = 4/3$:
$$\frac{T_{longest}}{T_{shortest}} = \frac{1 + 4/3}{1 + \frac{1}{2}(4/3)} = \frac{7/3}{1+2/3} = \frac{7/3}{5/3} = \frac{7}{5}$$