Source: Principles of Physics
Problem Sets:
Problem
A block with mass $m$ is connected to two identical masselss spring with hooke's constant $k$, as shown in the figure.
- Find the period of oscillation of the block.
- what if the springs are only only fixed on the wall, but detached from the block. Assuming the springs are at equilibrium when the block is at rest.
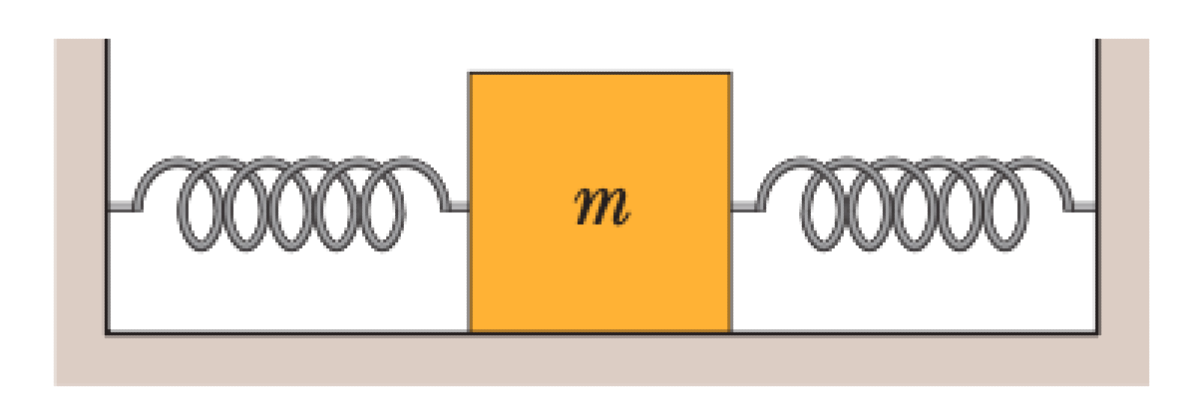
P0693-problem-1
[Q1] The period of oscillation when the block is attached to both springs is:
$$T = 2\pi\sqrt{\frac{m}{2k}}$$[Q2] The period of oscillation when the block is detached from the springs is:
$$T' = 2\pi\sqrt{\frac{m}{k}}$$[Q1] Find the period of oscillation of the block.
When the block is attached to both springs, displacing it from its equilibrium position causes both springs to exert a restoring force in the same direction. Let the equilibrium position be $x=0$. If the block is displaced by a distance $x$ to the right:
- The left spring is stretched by $x$ and pulls the block to the left with a force $F_L = -kx$.
- The right spring is compressed by $x$ and pushes the block to the left with a force $F_R = -kx$.
The net restoring force on the block is the sum of these two forces:
$$F_{net} = F_L + F_R = -kx - kx = -2kx$$This equation is in the form of Hooke's Law, $F_{net} = -k_{eff}x$, where the effective spring constant $k_{eff}$ is:
$$k_{eff} = 2k$$The system undergoes simple harmonic motion (SHM). The period of oscillation for a mass-spring system is given by:
$$T = 2\pi\sqrt{\frac{m}{k_{eff}}}$$Substituting the effective spring constant, we find the period:
$$T = 2\pi\sqrt{\frac{m}{2k}}$$[Q2] What if the springs are only fixed on the wall, but detached from the block?
In this case, the block is not attached to the springs and can only compress them. The springs do not exert a force when the block moves away from them (i.e., they cannot pull).
Let the equilibrium position be $x=0$, where the block is situated between the two springs at their natural lengths.
- When the block moves to the right ($x>0$), it compresses only the right spring. The left spring has no effect. The restoring force is $F_{net} = -kx$.
- When the block moves to the left ($x<0$), it compresses only the left spring. The right spring has no effect. The restoring force is again $F_{net} = -kx$.
In either case, the net restoring force on the block whenever it is displaced from equilibrium is $F_{net} = -kx$. This is the equation of motion for a simple harmonic oscillator with a single spring of constant $k$.
Therefore, the period of oscillation is that of a standard mass-spring system:
$$T' = 2\pi\sqrt{\frac{m}{k}}$$This motion consists of the block completing a half-cycle of SHM with one spring, followed by a half-cycle of SHM with the other spring. The period is the same as if it were attached to only one of the springs.