Source: Principles of Physics
Problem Sets:
Problem
As shown, the pendulum consists of a uniform disk with radius $r = 10.0$ cm and mass $m_d = 500$ g attached to a uniform rod with length $L = 500$ mm and mass $m_r = 270$ g. The rod is pivoted at its upper end.
- Calculate the rotational inertia of the pendulum about the pivot point.
- What is the distance between the pivot point and the center of mass of the pendulum?
- Calculate the period of oscillation.
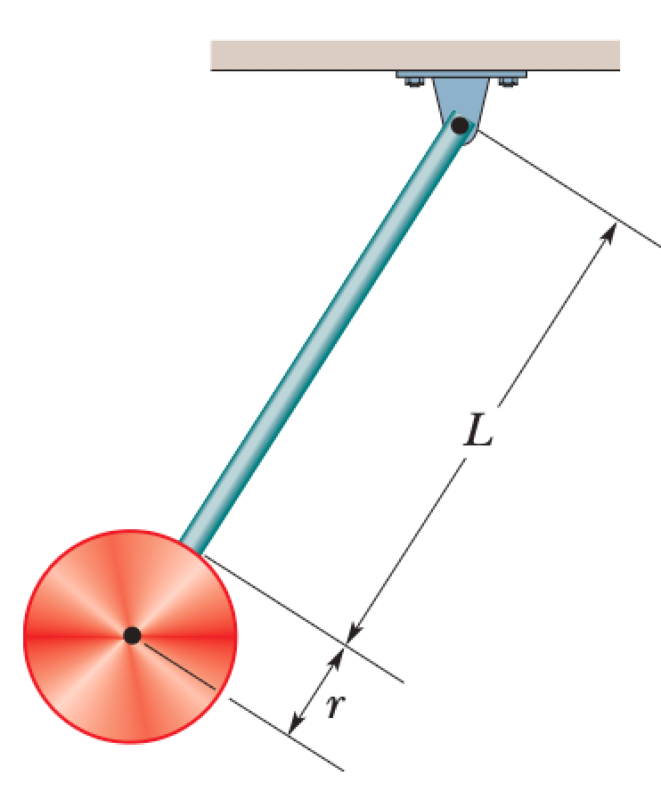
P0690-problem-1
[Q1] $I_P = 0.205$ kg$\cdot$m$^2$ [Q2] $h = 0.477$ m [Q3] $T = 1.50$ s
Let the pivot be P. The total rotational inertia $I_P$ is the sum of the inertia of the rod and the disk about P. The rod's inertia about its end is $I_{r,P} = \frac{1}{3}m_r L^2$. The disk's inertia about its center of mass is $I_{d,cm} = \frac{1}{2}m_d r^2$. The distance from P to the disk's center is $d_{disk} = L+r$. By the parallel-axis theorem, $I_{d,P} = I_{d,cm} + m_d d_{disk}^2 = \frac{1}{2}m_d r^2 + m_d(L+r)^2$. [Q1] The total inertia is $I_P = I_{r,P} + I_{d,P} = \frac{1}{3}m_r L^2 + \frac{1}{2}m_d r^2 + m_d(L+r)^2$.
$I_P = \frac{1}{3}(0.270 \text{ kg})(0.500 \text{ m})^2 + \frac{1}{2}(0.500 \text{ kg})(0.100 \text{ m})^2 + (0.500 \text{ kg})(0.500 \text{ m} + 0.100 \text{ m})^2 = 0.205 \text{ kg} \cdot \text{m}^2$.[Q2] The distance $h$ from the pivot to the combined center of mass (CM) is found by treating the rod and disk as point masses at their respective CMs ($L/2$ and $L+r$).
$$h = \frac{m_r(L/2) + m_d(L+r)}{m_r + m_d}$$ $$h = \frac{(0.270 \text{ kg})(0.500 \text{ m}/2) + (0.500 \text{ kg})(0.500 \text{ m} + 0.100 \text{ m})}{0.270 \text{ kg} + 0.500 \text{ kg}} = 0.477 \text{ m}$$[Q3] The period of a physical pendulum is $T = 2\pi\sqrt{I/(Mgh)}$, where $M = m_r + m_d$.
$$T = 2\pi\sqrt{\frac{I_P}{(m_r+m_d)gh}}$$ $$T = 2\pi\sqrt{\frac{0.205 \text{ kg} \cdot \text{m}^2}{(0.770 \text{ kg})(9.8 \text{ m/s}^2)(0.477 \text{ m})}} = 1.50 \text{ s}$$