Source: Principles of Physics
Problem Sets:
Problem
A wheel is free to rotate about its fixed axle. A spring is attached to one of its spokes a distance $r$ from the axle, as shown in the figure.
- Assuming that the wheel is a hoop of mass $m$ and radius $R$, what is the angular frequency $\omega$ of small oscillations of this system in terms of $m, R, r,$ and the spring constant $k$?
- What is $\omega$ if $r=R$?
- What is $\omega$ if $r=0$?
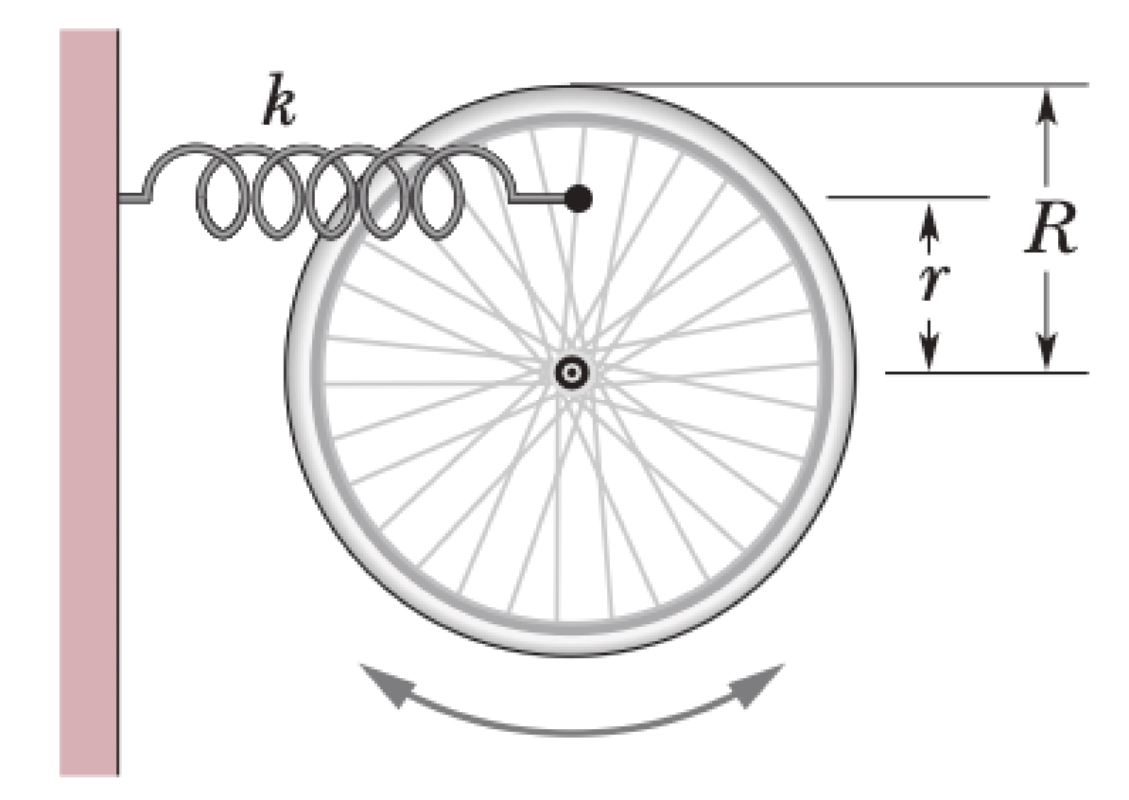
P0686-problem-1
[Q1] $\omega = \frac{r}{R}\sqrt{\frac{k}{m}}$ [Q2] $\omega = \sqrt{\frac{k}{m}}$ [Q3] $\omega = 0$
For small angular displacements $\theta$, the spring stretches by a distance $x \approx r\theta$. The spring exerts a restoring force $F_s = -kx = -kr\theta$. This force creates a restoring torque $\tau$ about the axle.
$$\tau = F_s \cdot r = (-kr\theta)r = -kr^2\theta$$The equation for rotational motion is $\tau = I\alpha$, where $I$ is the moment of inertia and $\alpha = d^2\theta/dt^2$ is the angular acceleration. For a hoop rotating about its center, $I = mR^2$.
$$I\alpha = -kr^2\theta$$ $$mR^2\alpha = -kr^2\theta$$ $$\alpha = -\frac{kr^2}{mR^2}\theta$$This is the equation for simple harmonic motion, $\alpha = -\omega^2\theta$, with the angular frequency $\omega$ given by:
$$\omega = \sqrt{\frac{kr^2}{mR^2}} = \frac{r}{R}\sqrt{\frac{k}{m}}$$For the case $r=R$, the expression simplifies. For the case $r=0$, the spring is attached at the axle, creates no torque, and thus no oscillation.