Source: Principles of Physics
Problem Sets:
Problem
A 2.50 kg disk of diameter $D = 42.0$ cm is supported by a rod of length $L = 76.0$ cm and negligible mass that is pivoted at its end.
- With the massless torsion spring unconnected, what is the period of oscillation?
- With the torsion spring connected, the rod is vertical at equilibrium. What is the torsion constant of the spring if the period of oscillation has been decreased by 0.500 s?
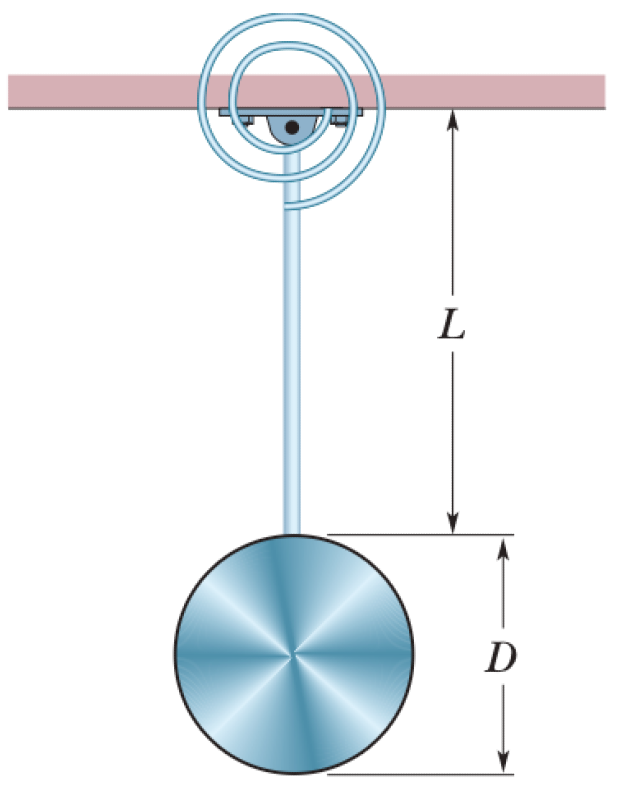
P0683-problem-1
[Q1] 2.00 s [Q2] 18.4 N m/rad
The system is a physical pendulum. The distance from the pivot to the center of mass (the disk's center) is $d=L+R=L+D/2$. By the parallel axis theorem, the moment of inertia about the pivot is $I = I_{cm} + md^2 = \frac{1}{2}mR^2 + m(L+R)^2$.
[Q1] Without the spring, the period $T_p$ is:
$$T_p = 2\pi \sqrt{\frac{I}{mgd}} = 2\pi \sqrt{\frac{\frac{1}{2}mR^2 + m(L+R)^2}{mg(L+R)}} = 2\pi \sqrt{\frac{R^2/2 + (L+R)^2}{g(L+R)}}$$[Q2] With the spring, the total restoring torque for a small angle $\theta$ is $\tau = -(mgd)\theta - \kappa\theta = -(mgd + \kappa)\theta$. The equation of motion is $I\ddot{\theta} = \tau$. The new period $T_{new}$ is:
$$T_{new} = 2\pi \sqrt{\frac{I}{mgd + \kappa}}$$Given $T_{new} = T_p - \Delta t$, where $\Delta t = 0.500$ s, we solve for the torsion constant $\kappa$:
$$mgd + \kappa = \frac{4\pi^2 I}{T_{new}^2} \implies \kappa = \frac{4\pi^2 I}{(T_p - \Delta t)^2} - mgd$$