Source: Principles of Physics
Problem Sets:
Problem
An overhead view shows a long uniform rod of mass 0.600 kg free to rotate in a horizontal plane about a vertical axis through its center. A spring with force constant k = 1850 N/m is connected horizontally between one end of the rod and a fixed wall. In equilibrium, the rod is parallel to the wall, and the spring is perpendicular to the rod.
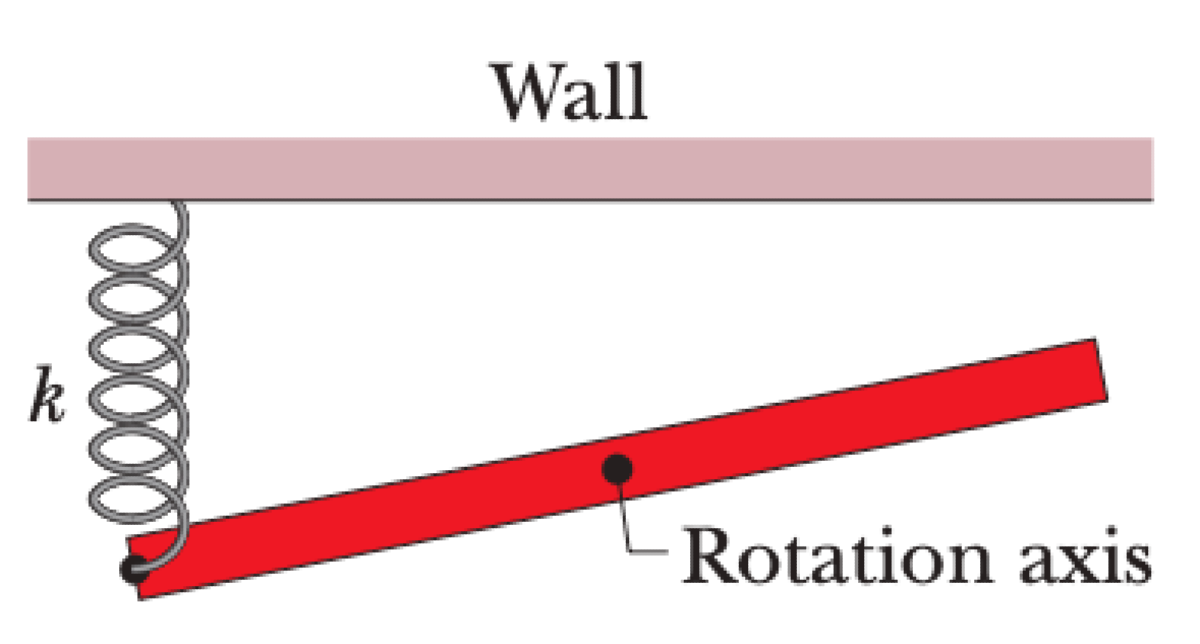
P0681-problem-1
[Q1] T = 0.0653 s
The period of angular SHM is $T = 2\pi\sqrt{I/\kappa}$. The moment of inertia of a rod of length $L$ rotating about its center is $I = \frac{1}{12}mL^2$.
For a small angular displacement $\theta$, the end of the rod moves a distance $x \approx (L/2)\theta$, stretching the spring. The spring exerts a restoring force $F = kx = k(L/2)\theta$. The force is nearly perpendicular to the rod, with a lever arm of $L/2$. The restoring torque is $\tau = -F(L/2) = -[k(L/2)\theta](L/2) = -k(L/2)^2\theta$. The torsional constant is $\kappa = k(L/2)^2$.
The period of oscillation is:
$$T = 2\pi\sqrt{\frac{I}{\kappa}} = 2\pi\sqrt{\frac{\frac{1}{12}mL^2}{k(L/2)^2}} = 2\pi\sqrt{\frac{mL^2/12}{kL^2/4}} = 2\pi\sqrt{\frac{m}{3k}}$$The length $L$ cancels out.
$$T = 2\pi\sqrt{\frac{0.600 \text{ kg}}{3(1850 \text{ N/m})}} = 0.0653 \text{ s}$$