Source: Principles of Physics
Problem Sets:
Problem
A 3.00 kg cube with edge lengths d = 6.00 cm is mounted on an axle through its center. A spring (k = 1200 N/m) connects the cube's upper corner to a rigid wall. Initially, the spring is horizontal and at its rest length. The cube is then rotated 3° and released.
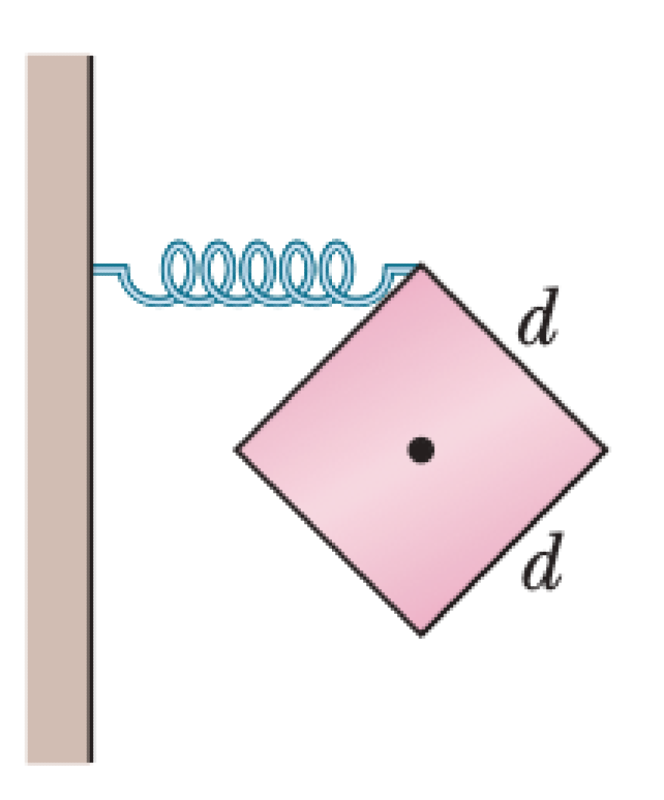
P0680-problem-1
[Q1] T = 0.257 s
The period of angular simple harmonic motion is $T = 2\pi\sqrt{I/\kappa}$, where $I$ is the moment of inertia and $\kappa$ is the torsional constant from the restoring torque $\tau = -\kappa\theta$.
For a small rotation $\theta$, the horizontal displacement of the corner is $x \approx (d/2)\theta$. The spring force is $F_s = kx = k(d/2)\theta$. The lever arm for this horizontal force is the vertical distance to the pivot, $y \approx d/2$. The restoring torque is $\tau = -F_s y \approx -[k(d/2)\theta](d/2) = -k(d/2)^2\theta$. Thus, the torsional constant is $\kappa = k(d/2)^2$.
The moment of inertia of a cube of mass $m$ and side $d$ rotating about an axis through its center and perpendicular to a face is $I = \frac{1}{6}md^2$.
The period is:
$$T = 2\pi\sqrt{\frac{I}{\kappa}} = 2\pi\sqrt{\frac{\frac{1}{6}md^2}{k(d/2)^2}} = 2\pi\sqrt{\frac{md^2/6}{kd^2/4}} = 2\pi\sqrt{\frac{2m}{3k}}$$ $$T = 2\pi\sqrt{\frac{2(3.00 \text{ kg})}{3(1200 \text{ N/m})}} = 0.257 \text{ s}$$