Source: Principles of Physics
Problem Sets:
Problem
A rectangular block, with face lengths $a = 35$ cm and $b = 45$ cm, is suspended on a thin horizontal rod running through a narrow hole in the block. The block swings about the rod like a physical pendulum. The hole is at a distance $r$ from the block's center, along a line connecting the center with a corner.
- Plot the period versus distance $r$ along that line such that the minimum in the curve is apparent.
- For what value of $r$ does that minimum occur?
- There is a line of points around the block's center for which the period of swinging has the same minimum value. What shape does that line make?
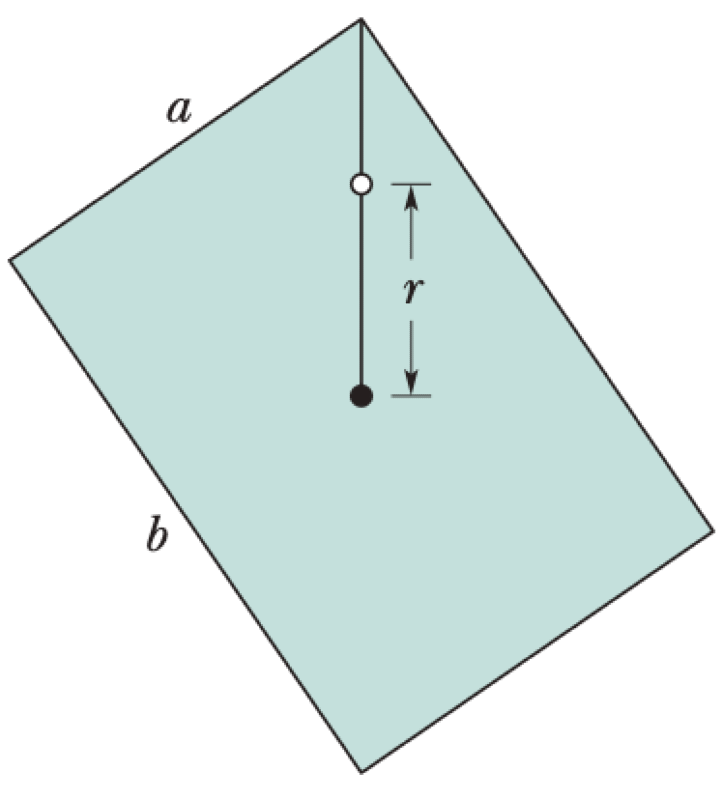
P0677-problem-2
[Q2] $r = 16.5$ cm [Q3] A circle
The period of a physical pendulum is given by $T = 2\pi\sqrt{I / (mgr)}$, where $I$ is the moment of inertia about the pivot, $m$ is the mass, and $r$ is the distance from the pivot to the center of mass.
The moment of inertia of a rectangular block about its center of mass is $I_{cm} = \frac{1}{12}m(a^2 + b^2)$. Using the parallel axis theorem, the moment of inertia about the pivot point is $I = I_{cm} + mr^2$.
Substituting $I$ into the period equation:
$$T(r) = 2\pi\sqrt{\frac{I_{cm} + mr^2}{mgr}} = 2\pi\sqrt{\frac{\frac{1}{12}m(a^2 + b^2) + mr^2}{mgr}}$$ $$T(r) = 2\pi\sqrt{\frac{\frac{a^2+b^2}{12} + r^2}{gr}}$$To find the minimum period, we must minimize the term inside the square root. This is equivalent to minimizing the function $f(r) = \frac{k^2+r^2}{r} = \frac{k^2}{r} + r$, where $k^2 = \frac{a^2+b^2}{12}$. The minimum value of this function occurs when the two terms are equal, $r = k^2/r$, which gives $r = k$.
Thus, the period is minimum when $r$ is equal to the radius of gyration about the center of mass:
$$r_{min} = \sqrt{\frac{a^2+b^2}{12}}$$Substituting the given values, with $a = 0.35$ m and $b = 0.45$ m:
$$r_{min} = \sqrt{\frac{(0.35 \text{ m})^2 + (0.45 \text{ m})^2}{12}} = \sqrt{\frac{0.1225 \text{ m}^2 + 0.2025 \text{ m}^2}{12}} = \sqrt{\frac{0.325 \text{ m}^2}{12}} \approx 0.165 \text{ m}$$Since the value of $r_{min}$ depends only on the moment of inertia and mass (properties of the body) and not on the direction from the center of mass, any pivot point at this distance $r_{min}$ from the center will result in the same minimum period. The locus of all such points forms a circle.