Source: Principles of Physics
Problem Sets:
Problem
Two blocks, with masses $m$ and $M$, are arranged on a horizontal frictionless surface as shown. The larger block $M$ is attached to a horizontal spring with spring constant $k$. The smaller block $m$ rests on top of $M$. The coefficient of static friction between the two blocks is $\mu_s$. The system undergoes simple harmonic motion (SHM).
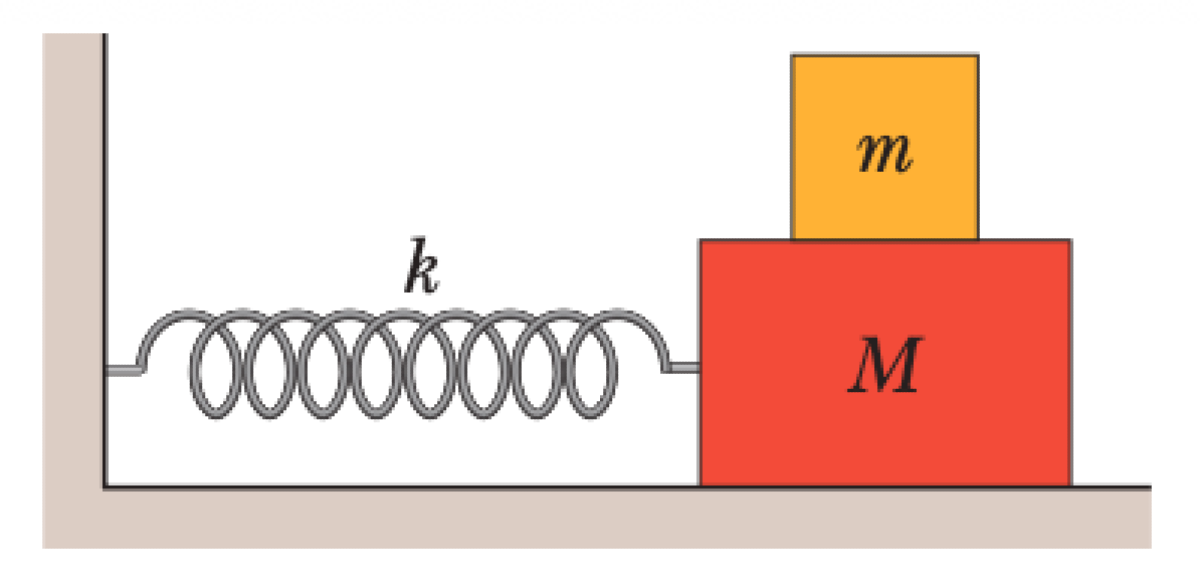
P0674-problem-1
A = \frac{\mu_s g (m+M)}{k}
For the two blocks to move together without slipping, the static friction force $f_s$ must provide the acceleration for the top block, $m$. According to Newton's second law for block $m$:
$$f_s = ma$$The maximum possible static friction force is $f_{s,max} = \mu_s N = \mu_s mg$. This maximum force corresponds to the maximum possible acceleration, $a_{max}$, of block $m$.
$$f_{s,max} = ma_{max} \implies \mu_s mg = ma_{max}$$ $$a_{max} = \mu_s g$$The system of both blocks (total mass $m+M$) undergoes SHM. The acceleration in SHM is given by $a = -\omega^2 x$. The magnitude of the acceleration is maximum at the amplitude, $x = A$:
$$a_{max} = \omega^2 A$$The angular frequency $\omega$ for the combined system is:
$$\omega^2 = \frac{k}{m+M}$$To prevent slipping, the maximum acceleration of the system must not exceed the maximum acceleration that static friction can provide to block $m$. Setting the two expressions for $a_{max}$ equal:
$$\mu_s g = \omega^2 A = \left(\frac{k}{m+M}\right)A$$Solving for the amplitude $A$:
$$A = \frac{\mu_s g (m+M)}{k}$$