Source: Principles of Physics
Problem Sets:
Problem
A block of mass $m$ (and weight $W=mg$) can slide without friction on an incline at an angle $\theta$. It is connected to the top of the incline by a massless spring of unstretched length $L_0$ and spring constant $k$.
- How far from the top of the incline is the block's equilibrium point?
- If the block is pulled slightly down the incline and released, what is the period of the resulting oscillations?
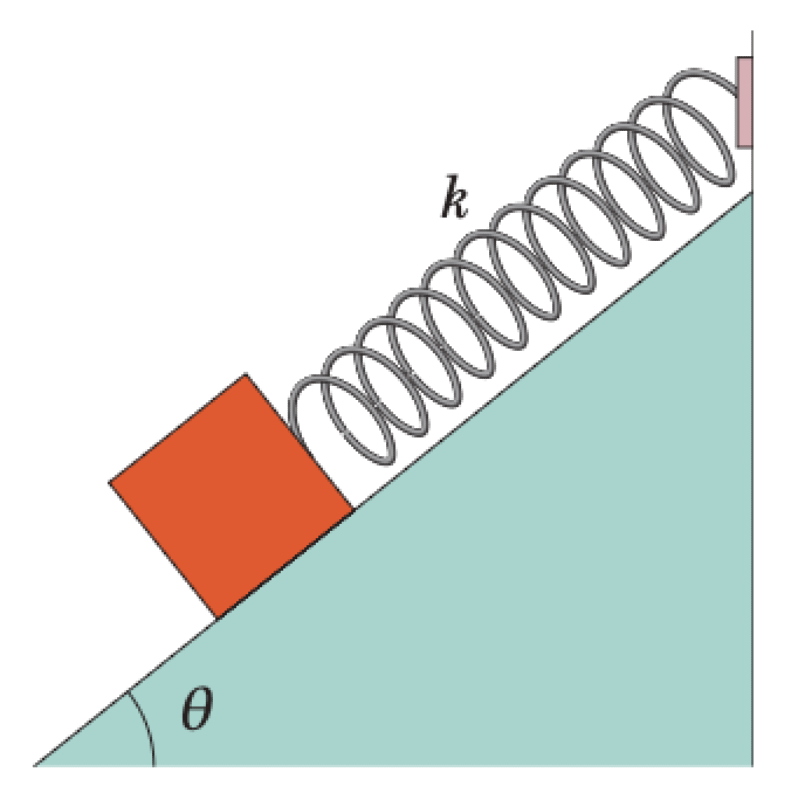
P0673-problem-1
[Q1] $L_{eq} = L_0 + \frac{mg \sin\theta}{k}$ [Q2] $T = 2\pi \sqrt{\frac{m}{k}}$
[Q1] At the equilibrium position, the net force on the block is zero. The downward force along the incline due to gravity is balanced by the upward spring force. Let the extension of the spring from its unstretched length be $\Delta L$.
$$F_{net} = F_s - mg \sin\theta = 0$$ $$k \Delta L = mg \sin\theta$$Solving for the extension:
$$\Delta L = \frac{mg \sin\theta}{k}$$The total distance from the top of the incline, $L_{eq}$, is the sum of the unstretched length and the extension.
$$L_{eq} = L_0 + \Delta L = L_0 + \frac{mg \sin\theta}{k}$$[Q2] For oscillations, consider the block displaced by a distance $x$ down the incline from its equilibrium position. The total spring extension is now $\Delta L + x$. The net force along the incline is:
$$F_{net} = mg \sin\theta - k(\Delta L + x)$$From the equilibrium condition, we know $mg \sin\theta = k \Delta L$. Substituting this into the force equation:
$$F_{net} = k \Delta L - k(\Delta L + x) = -kx$$This is the restoring force for simple harmonic motion, $F = -k_{eff}x$, with an effective spring constant $k_{eff} = k$. The period of oscillation $T$ is independent of gravity and the incline angle.
$$T = 2\pi \sqrt{\frac{m}{k_{eff}}} = 2\pi \sqrt{\frac{m}{k}}$$