Source: Principles of Physics
Problem Sets:
Problem
Block 1 of mass $m_1$ slides on a frictionless elevated surface at speed $v_{1i}$. It undergoes a one-dimensional elastic collision with a stationary block 2. After the collision, block 2, which is attached to a spring of constant $k$, oscillates in SHM with period $T$. Block 1 slides off the surface, which is at a height $h$ above the ground.
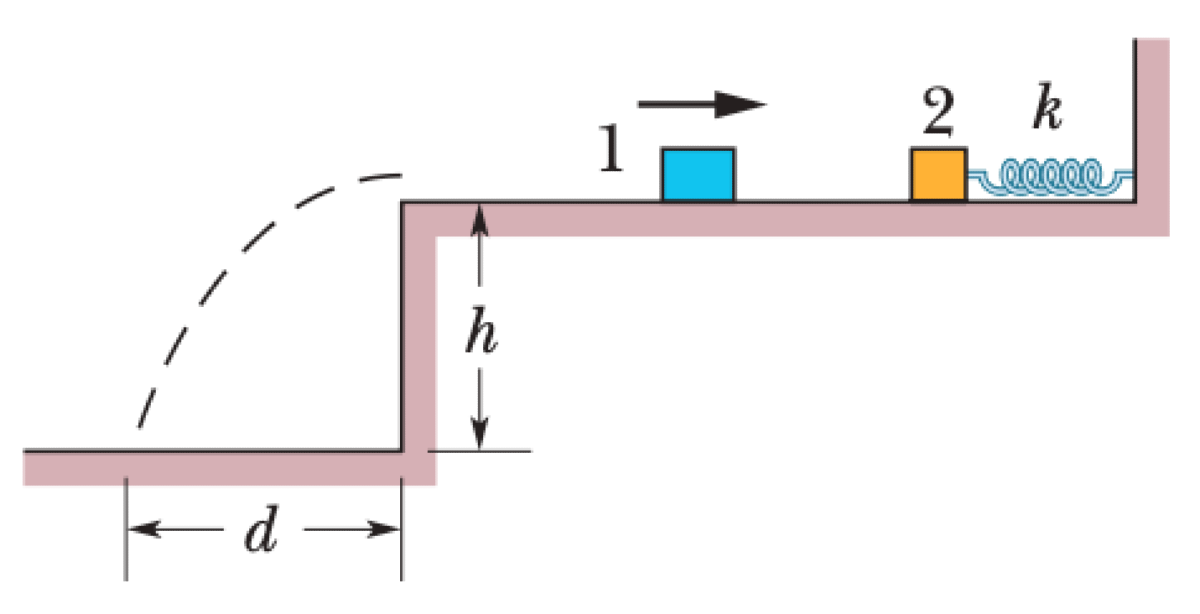
P0670-problem-1
The mass of block 2, $m_2$, can be determined from the period of its simple harmonic motion. The period of a mass-spring system is $T = 2\pi\sqrt{m_2/k}$.
$$m_2 = k \left(\frac{T}{2\pi}\right)^2$$For a 1D elastic collision with a stationary target, the final velocity of the incident particle (block 1), $v_{1f}$, is given by conservation of momentum and kinetic energy:
$$v_{1f} = \left(\frac{m_1 - m_2}{m_1 + m_2}\right) v_{1i}$$After leaving the surface, block 1 undergoes projectile motion. The time of flight $t$ is found from the vertical motion under gravity $g$:
$$h = \frac{1}{2}gt^2 \implies t = \sqrt{\frac{2h}{g}}$$The horizontal range $d$ is the product of the constant horizontal velocity $v_{1f}$ and the time of flight $t$:
$$d = v_{1f} t = \left(\frac{m_1 - m_2}{m_1 + m_2}\right) v_{1i} \sqrt{\frac{2h}{g}}$$Substituting the expression for $m_2$ gives the range in terms of the initial parameters.