Source: Principles of Physics
Problem Sets:
Problem
A uniform board of mass $m$ and length $L$ is hinged at one end. The other end is attached to a vertical spring with spring constant $k$. After a penguin dives off, the board oscillates with a small amplitude.
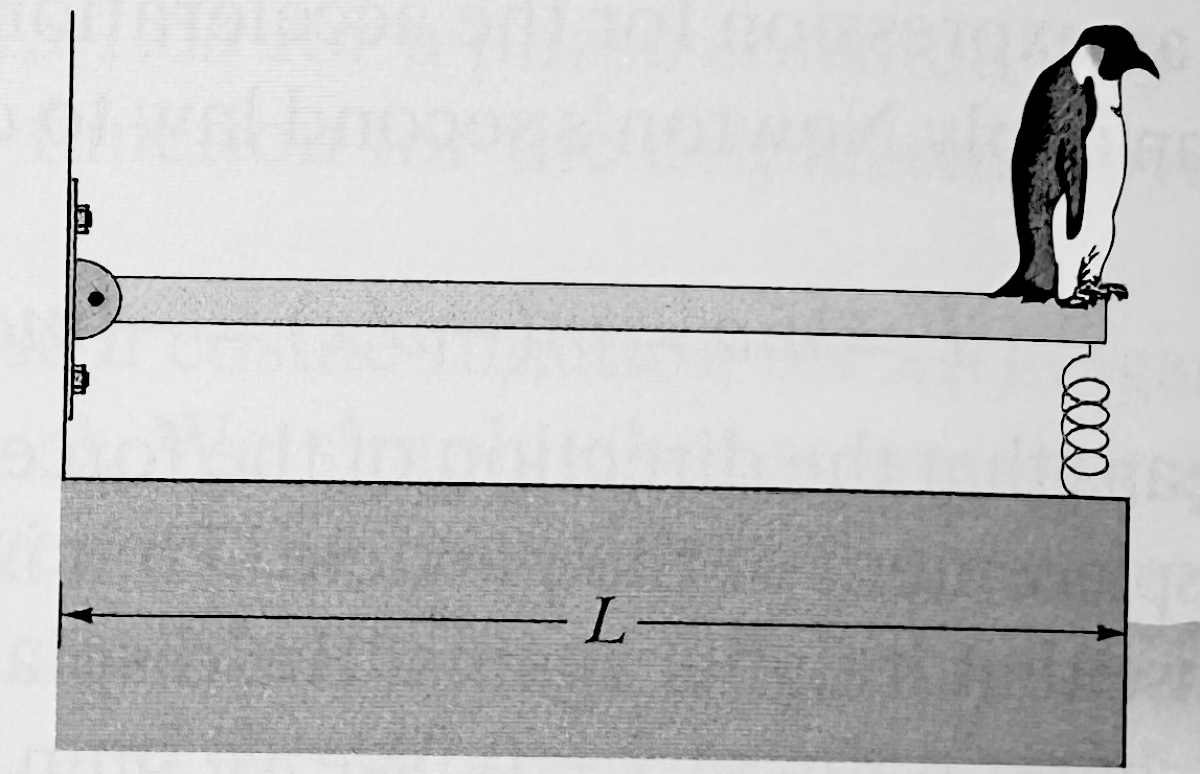
P0667-problem-1
T = 2\pi\sqrt{\frac{m}{3k}}
The board undergoes rotational simple harmonic motion about the hinge. We can find the period using the rotational form of Newton's second law, $\tau = I\alpha$.
First, determine the net restoring torque for a small angular displacement $\theta$ from the equilibrium position. The change in the spring's vertical displacement is $\Delta y = L \sin\theta \approx L\theta$ for small angles. The restoring force is $\Delta F = -k \Delta y = -kL\theta$. This force acts at a distance $L$ from the pivot, so the restoring torque is:
$$\tau = (\Delta F)L = (-kL\theta)L = -kL^2\theta$$This is of the form $\tau = -\kappa \theta$, where the effective torsional constant is $\kappa = kL^2$.
Next, find the moment of inertia $I$ of the uniform board about the hinge (one end). Using the parallel-axis theorem or the standard formula for a rod about its end:
$$I = \frac{1}{3}mL^2$$The equation of motion is $I\alpha = \tau$, which means $I\frac{d^2\theta}{dt^2} = -\kappa\theta$. The angular frequency is $\omega = \sqrt{\kappa/I}$, and the period is $T = 2\pi/\omega$.
$$T = 2\pi\sqrt{\frac{I}{\kappa}}$$Substituting the expressions for $I$ and $\kappa$:
$$T = 2\pi\sqrt{\frac{\frac{1}{3}mL^2}{kL^2}} = 2\pi\sqrt{\frac{m}{3k}}$$