Source: High school physics (Chinese)
Problem
As shown in Figure, a uniform sphere A of weight $G_A = 10$ N and a uniform cubic block B of weight $G_B = 20$ N are placed on a fixed inclined plane with an angle $\alpha=30^\circ$. The sphere's diameter and the cube's side length are both $2R=0.2$ m. A horizontal force $P=15$ N acts on block B, parallel to the base of the incline. The system is in static equilibrium.
- Find the magnitude and direction of the friction forces exerted by the inclined plane on A and B.
- Find the distance between the line of action of the resultant normal force $N_B$ on B and the center of mass O' of B.
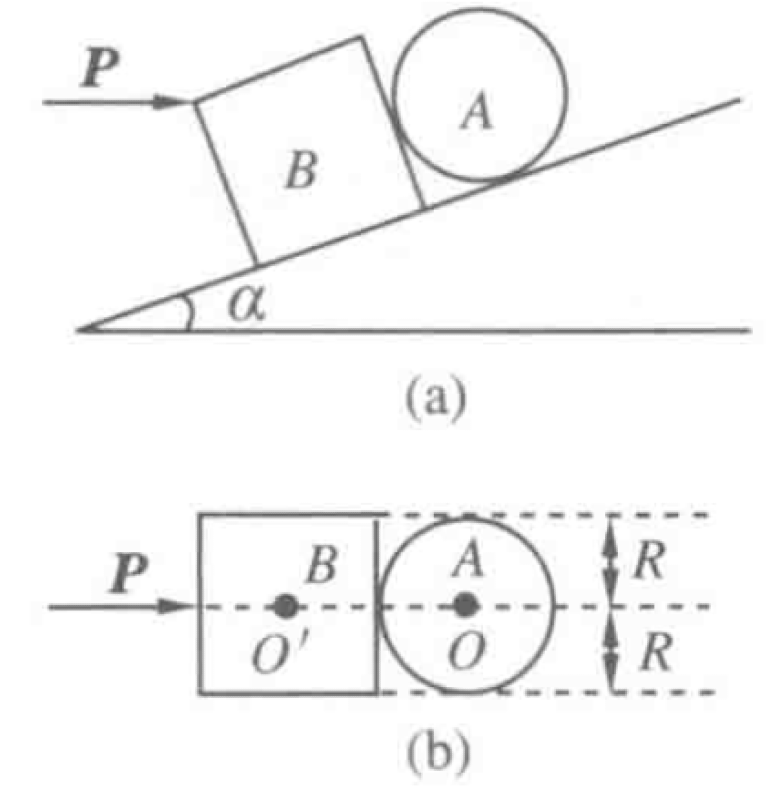
P0655-problem-1
[Q1] $|f_A| = 5\sqrt{2} \approx 7.07$ N; $|f_B| = 10\sqrt{2} \approx 14.14$ N. Both are directed up the slope at $45^\circ$ relative to the line of steepest descent, away from the side where P is applied. [Q2] $d \approx 0.0817$ m
Let the coordinate system be x-axis down the slope, y-axis normal to the slope, and z-axis horizontal along the slope. The system is statically indeterminate. A common physical assumption is that the required coefficient of friction is the same for both bodies: $\mu_A = \mu_B$, which means $|f_A|/N_A = |f_B|/N_B$.
The normal forces are $N_A = G_A\cos\alpha = 10\cos30^\circ = 5\sqrt{3}$ N, and $N_B = G_B\cos\alpha = 20\cos30^\circ = 10\sqrt{3}$ N. Let $N_{AB}$ be the magnitude of the contact force between A and B (along z-axis). Force equilibrium on A: The driving forces are $G_A\sin\alpha$ (x-dir) and $N_{AB}$ (z-dir). The friction $f_A$ opposes their vector sum. Force equilibrium on B: The driving forces are $G_B\sin\alpha$ (x-dir) and $P-N_{AB}$ (z-dir). The friction $f_B$ opposes their vector sum.
$|f_A| = \sqrt{(G_A\sin\alpha)^2 + N_{AB}^2}$ and $|f_B| = \sqrt{(G_B\sin\alpha)^2 + (P-N_{AB})^2}$.From the friction assumption: $\frac{\sqrt{(10\cdot0.5)^2 + N_{AB}^2}}{5\sqrt{3}} = \frac{\sqrt{(20\cdot0.5)^2 + (15-N_{AB})^2}}{10\sqrt{3}}$. Solving this gives $N_{AB}^2 + 10N_{AB} - 75 = 0$, which yields the positive root $N_{AB} = 5$ N.
[Q1] For A, the driving force is $(5, 5)$ N. Friction $f_A = (-5, -5)$ N. $|f_A| = \sqrt{5^2+5^2} = 5\sqrt{2}$ N. For B, the driving force is $(10, 15-5) = (10, 10)$ N. Friction $f_B = (-10, -10)$ N. $|f_B| = \sqrt{10^2+10^2} = 10\sqrt{2}$ N. The direction for both is up the slope at $45^\circ$ to the line of steepest descent.
[Q2] For rotational equilibrium of B about its center of mass O', the net torque is zero. Assume the lines of action of $P$ and $N_{AB}$ pass through O'. The torque from the ground reaction force (normal force $N_B$ and friction $f_B$) must be zero. Assume the center of pressure and center of friction coincide at a point $(x_p, -R, z_p)$ relative to O'. The torque is $\vec{\tau} = \vec{r} \times (\vec{N}_B + \vec{f}_B) = 0$.
$\vec{r}=(x_p, -R, z_p)$, $\vec{N}_B=(0, 10\sqrt{3}, 0)$ N, $\vec{f}_B=(-10, 0, -10)$ N.The cross product yields three component equations:
$10R - 10\sqrt{3} z_p = 0 \implies z_p = R/\sqrt{3}$ $-10z_p + 10x_p = 0 \implies x_p = z_p$ $10\sqrt{3} x_p - 10R = 0 \implies x_p = R/\sqrt{3}$The equations are consistent. The normal force $N_B$ acts at $(x_p, z_p) = (R/\sqrt{3}, R/\sqrt{3})$ on the base plane. The distance $d$ from O' to the line of action of $N_B$ is $d=\sqrt{x_p^2 + z_p^2}$.
$d = \sqrt{(R/\sqrt{3})^2 + (R/\sqrt{3})^2} = \sqrt{2R^2/3} = R\sqrt{2/3}$.Given $2R=0.2$ m, so $R=0.1$ m.
$d = 0.1 \sqrt{2/3} \approx 0.0817$ m.