Source: High school physics (Chinese)
Problem
A rod of mass $m=50$ kg and length $L$ stands on a horizontal surface with a coefficient of maximum static friction $\mu=0.3$. The top of the rod is held by a rope fixed to the ground, making an angle $\theta=30^\circ$ with the rod, as shown in Figure. A horizontal force $F$ is applied to the rod at a height $h$ from the ground.
- If $h=2L/5$, what is the maximum value of $F$ before the rod slips?
- What is the situation if the point of application is moved to $h=4L/5$?
- For what values of $h$ will the rod never slip, regardless of the magnitude of $F$?
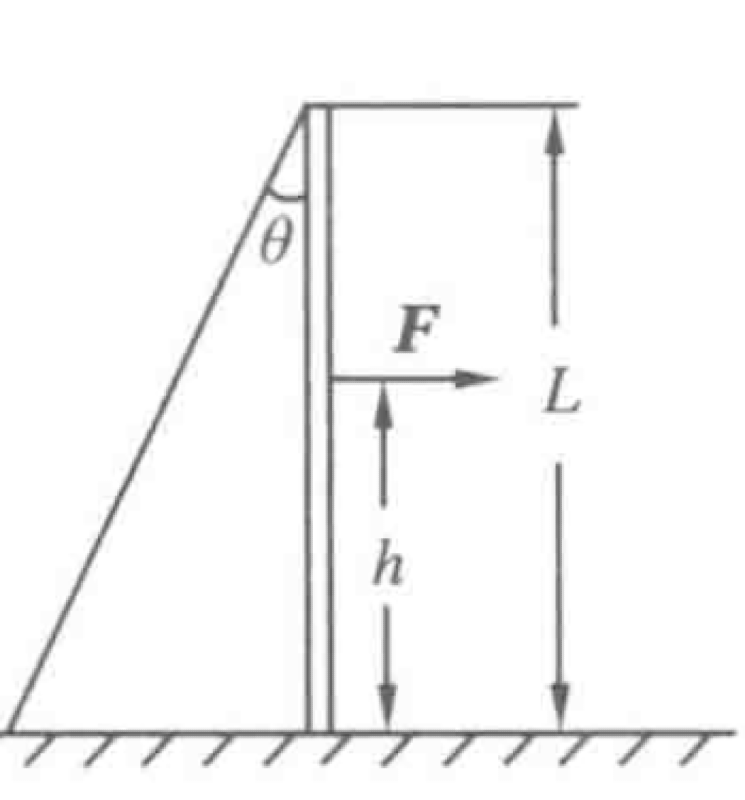
P0654-problem-1
[Q1] $F_{max} \approx 383$ N [Q2] The rod will not slip for any positive force $F$. [Q3] $h \ge 0.658L$
Let the forces on the rod be the applied force $F$, weight $W=mg$, rope tension $T$, ground normal force $N$, and static friction $f$. For static equilibrium, the net force and net torque are zero. Taking torques about the base of the rod:
$$\Sigma \tau = T_x L - Fh = (T \sin\theta)L - Fh = 0 \implies T\sin\theta = \frac{Fh}{L}$$The horizontal and vertical force equilibrium equations are:
$$\Sigma F_x = F - f - T\sin\theta = 0$$ $$\Sigma F_y = N - W - T\cos\theta = 0$$At the point of slipping, $f = f_{max} = \mu N$. Substituting for $f$ and $T\sin\theta$:
$$F_{max}(1 - \frac{h}{L}) = \mu N$$From the vertical force equation, $N = W + T\cos\theta = W + (T\sin\theta)\cot\theta = W + \frac{F_{max}h}{L}\cot\theta$. Substitute $N$ into the friction equation:
$$F_{max}(1 - \frac{h}{L}) = \mu (mg + \frac{F_{max}h}{L}\cot\theta)$$ $$F_{max} \left( 1 - \frac{h}{L} - \frac{\mu h}{L}\cot\theta \right) = \mu mg$$ $$F_{max} = \frac{\mu mg}{1 - \frac{h}{L}(1 + \mu\cot\theta)}$$The rod will not slip for any $F > 0$ if the denominator is less than or equal to zero. This occurs when:
$$1 - \frac{h}{L}(1 + \mu\cot\theta) \le 0 \implies h \ge \frac{L}{1 + \mu\cot\theta}$$Using $g=10$ m/s$^2$, $mg=500$ N. $\cot30^\circ=\sqrt{3}$.
[Q1] For $h = 2L/5$, $h/L = 0.4$.
$$F_{max} = \frac{0.3 \cdot 500}{1 - 0.4(1 + 0.3\sqrt{3})} = \frac{150}{1 - 0.4(1.52)} \approx 383 \text{ N}$$[Q2] The critical height is $h_c = \frac{L}{1 + 0.3\sqrt{3}} \approx 0.658L$. For $h=4L/5 = 0.8L$, we have $h > h_c$. The denominator in the expression for $F_{max}$ is negative, meaning the friction force available increases faster than the force required to prevent slipping. Thus, the rod will not slip for any applied force $F$.
[Q3] The rod will never slip when $h \ge h_c \approx 0.658L$.