Source: High school physics (Chinese)
Problem
As shown in Figure, a uniform thin wooden rod of length $l$ and density $\rho$ is suspended vertically by a thin string from its top end. A bucket of water (density $\rho_0$) is slowly lifted, gradually immersing the rod. When the length of the rod immersed in water exceeds a critical length $l'$, the rod becomes unstable and starts to tilt. Find $l'$.
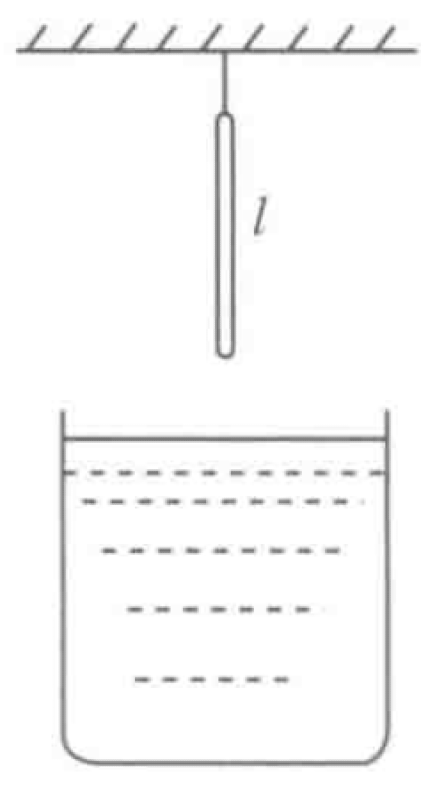
P0653-problem-1
The rod becomes unstable when a small angular displacement $\theta$ from the vertical results in a net torque that pushes it further from equilibrium. We analyze the torques about the suspension point P. The forces are the rod's weight $W$ and the buoyant force $F_B$.
- Weight $W = (\rho A l)g$ acts at the center of mass, a distance $l/2$ from P. It provides a restoring torque:
- Buoyant force $F_B = (\rho_0 A x)g$ acts at the center of buoyancy, which for an immersed length $x$ is a distance $(l - x/2)$ from P. It provides a toppling torque:
The critical point of stability is when the net torque is zero. Let the critical immersed length be $l'$.
$$\tau_{net} = \tau_W + \tau_B = 0$$ $$-\rho A g \frac{l^2}{2} + \rho_0 A g l'(l-\frac{l'}{2}) = 0$$Canceling $Ag$ and rearranging gives a quadratic equation for $l'$:
$$\frac{\rho_0}{2}(l')^2 - \rho_0 l (l') + \frac{\rho l^2}{2} = 0$$ $$\rho_0(l')^2 - 2\rho_0 l (l') + \rho l^2 = 0$$Using the quadratic formula:
$$l' = \frac{2\rho_0 l \pm \sqrt{(2\rho_0 l)^2 - 4(\rho_0)(\rho l^2)}}{2\rho_0} = l \pm \sqrt{l^2 - \frac{\rho}{\rho_0}l^2}$$ $$l' = l \left( 1 \pm \sqrt{1 - \frac{\rho}{\rho_0}} \right)$$Since the immersed length $l'$ must be less than the total length $l$, we take the minus sign. For $x > l'$, the toppling torque exceeds the restoring torque, causing instability.