Source: High school physics (Chinese)
Problem
As shown in Figure 5.32, a thin rod AB is connected to the ceiling by a hinge at A. Its lower end is hinged to another thin rod BC. The two rods have equal length, and their motion is restricted to the vertical plane shown. Friction at the hinges is negligible. An appropriate external force $\vec{F}$ is applied at C to keep the rods in equilibrium in the position shown, where the angle between the rods is $90^\circ$ and C is directly below A.
- Regardless of the masses of the two rods, what is the possible range of directions for the external force $\vec{F}$?
- If the mass of rod AB is $m_1 = 1.0$ kg and the mass of rod BC is $m_2 = 2.0$ kg, find the magnitude and direction of the external force $\vec{F}$.
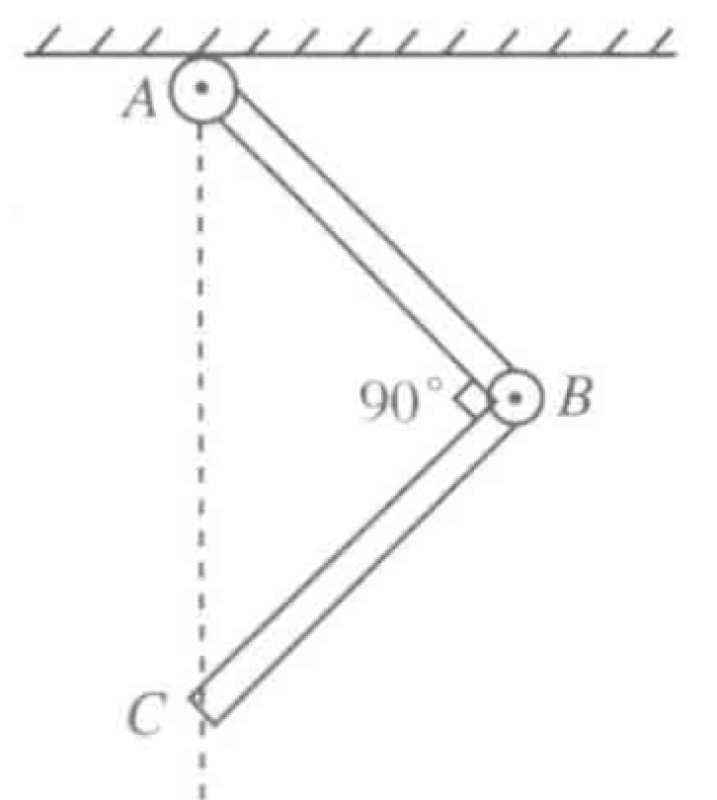
P0652-problem-1
[Q1] The force must be directed to the left, at an angle between $45^\circ$ below the horizontal and $45^\circ$ above the horizontal (i.e., in the angular range $[135^\circ, 225^\circ]$). [Q2] $F = \frac{\sqrt{10}}{4}g$; Direction is $\arctan(1/3)$ above the horizontal, pointing to the left.
Let the length of each rod be $L$. Let A be the origin (0,0). Given the geometry, B is at $(L/\sqrt{2}, -L/\sqrt{2})$ and C is at $(0, -L\sqrt{2})$. The center of mass of rod AB is $G_1 = (L/(2\sqrt{2}), -L/(2\sqrt{2}))$. The center of mass of rod BC is $G_2 = (L/(2\sqrt{2}), -3L/(2\sqrt{2}))$. The external force is $\vec{F} = (F_x, F_y)$.
Consider the entire system (AB + BC). For rotational equilibrium, the net torque about hinge A must be zero. The forces creating torques about A are gravity on AB ($m_1g$), gravity on BC ($m_2g$), and the applied force $\vec{F}$ at C.
$$\sum \tau_A = \vec{r}_{G1} \times (m_1\vec{g}) + \vec{r}_{G2} \times (m_2\vec{g}) + \vec{r}_C \times \vec{F} = 0$$Taking the z-components (out of page):
$$-\frac{L}{2\sqrt{2}}m_1g - \frac{L}{2\sqrt{2}}m_2g - L\sqrt{2}F_x = 0$$ $$F_x = -\frac{(m_1+m_2)g}{4}$$Now, consider rod BC alone. The net torque about hinge B must be zero.
$$\sum \tau_B = (\vec{r}_{G2}-\vec{r}_B) \times (m_2\vec{g}) + (\vec{r}_C-\vec{r}_B) \times \vec{F} = 0$$The z-components give:
$$\frac{L}{2\sqrt{2}}m_2g + \frac{L}{\sqrt{2}}(F_x - F_y) = 0$$ $$F_y = F_x + \frac{m_2g}{2}$$Substituting $F_x$:
$$F_y = -\frac{(m_1+m_2)g}{4} + \frac{m_2g}{2} = \frac{(m_2-m_1)g}{4}$$[Q1] The direction of $\vec{F}$ is given by $\tan\theta = F_y/F_x = \frac{m_1-m_2}{m_1+m_2}$. Since $m_1, m_2 > 0$, the ratio $\frac{m_1-m_2}{m_1+m_2}$ can range from -1 (for $m_1 \to 0$) to +1 (for $m_2 \to 0$). Since $F_x$ is always negative, the force vector must lie in the second and third quadrants, in the angular range from $135^\circ$ to $225^\circ$ with respect to the positive x-axis.
[Q2] Substitute $m_1 = 1.0$ kg and $m_2 = 2.0$ kg:
$$F_x = -\frac{(1.0+2.0)g}{4} = -0.75g$$ $$F_y = \frac{(2.0-1.0)g}{4} = 0.25g$$Magnitude:
$$F = \sqrt{F_x^2 + F_y^2} = \sqrt{(-0.75g)^2 + (0.25g)^2} = g\sqrt{0.5625+0.0625} = g\sqrt{0.625} = \frac{\sqrt{10}}{4}g$$Direction: Let $\alpha$ be the angle above the negative horizontal axis.
$$\tan\alpha = \frac{|F_y|}{|F_x|} = \frac{0.25g}{0.75g} = \frac{1}{3}$$ $$\alpha = \arctan(1/3)$$