Source: High school physics (Chinese)
Problem
A uniform rectangular block with base length a and height b is placed on an inclined plane. The coefficient of static friction between the plane and the block is $\mu$. The inclination angle of the plane, $\theta$, is gradually increased from zero. At some critical angle $\theta_0$, the block will either start to slide or to tip over.
- Find the critical angle $\theta_0$ for the block to start sliding.
- Find the critical angle $\theta_0$ for the block to start tipping over.
- State the conditions that determine whether the block will slide first or tip over first.
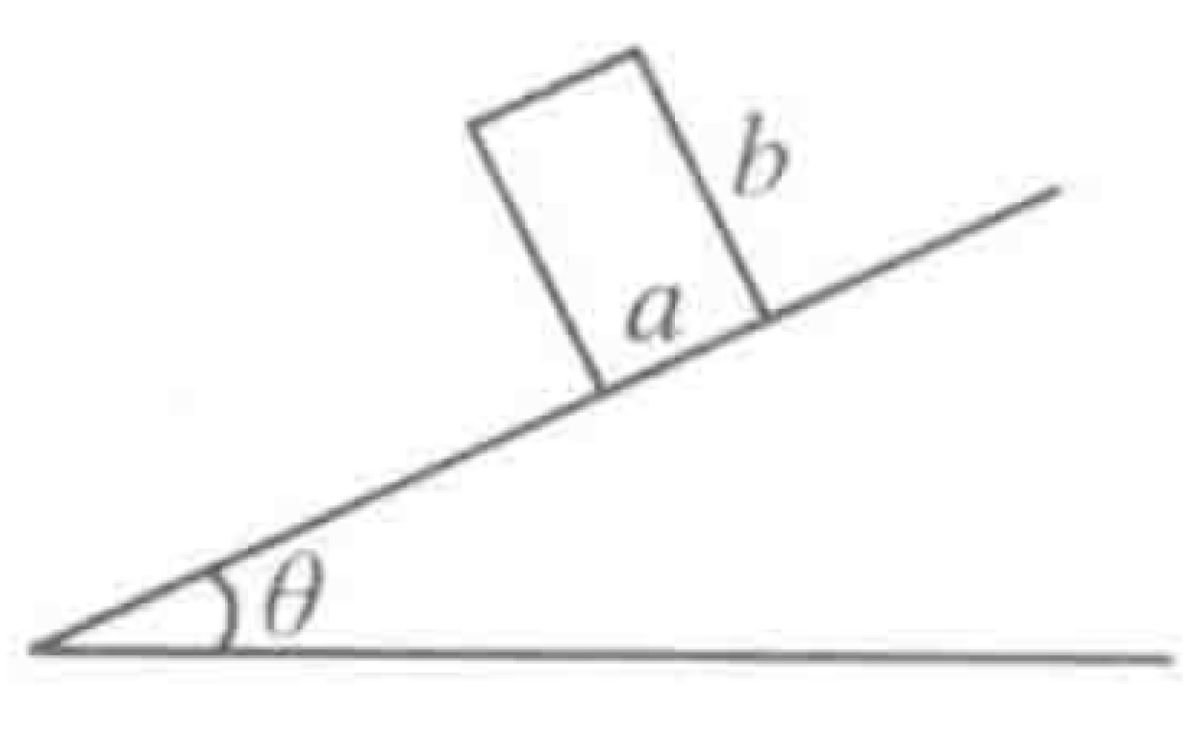
P0651-problem-1
[Q1] For sliding: $\theta_0 = \arctan(\mu)$ [Q2] For tipping: $\theta_0 = \arctan(a/b)$ [Q3] If $\mu < a/b$, the block slides first. If $\mu > a/b$, the block tips over first.
Let the weight of the block be W. The block will start to slide when the component of gravity parallel to the incline equals the maximum static friction force. The component of gravity parallel to the incline is $W \sin\theta$. The normal force is $N = W \cos\theta$. The maximum static friction is $f_{s,max} = \mu N = \mu W \cos\theta$. At the critical angle for sliding, $\theta_s$:
$$W \sin\theta_s = \mu W \cos\theta_s \implies \tan\theta_s = \mu$$The block will start to tip over about its lower corner when the vertical line of action of its weight W passes through this corner. At this point, the torque due to gravity tending to tip the block is equal to the restoring torque. Taking torques about the lower corner: Torque from parallel component of W: $\tau_{tip} = (W \sin\theta_t) \frac{b}{2}$ Torque from perpendicular component of W: $\tau_{restore} = (W \cos\theta_t) \frac{a}{2}$ At the critical angle for tipping, $\theta_t$, these torques are equal:
$$(W \sin\theta_t) \frac{b}{2} = (W \cos\theta_t) \frac{a}{2} \implies \tan\theta_t = \frac{a}{b}$$The block will undergo the motion that occurs at the smaller angle. If $\theta_s < \theta_t$, it slides first. This corresponds to $\tan\theta_s < \tan\theta_t$, which means $\mu < a/b$. If $\theta_t < \theta_s$, it tips first. This corresponds to $\tan\theta_t < \tan\theta_s$, which means $a/b < \mu$.