Source: High school physics (Chinese)
Problem
As shown in Figure, a uniform chain of weight G is hung on two hooks of equal height. The ends of the chain make an angle $\theta$ with the horizontal.
- Find the force exerted on the ends of the chain.
- Find the tension at the lowest point of the chain.
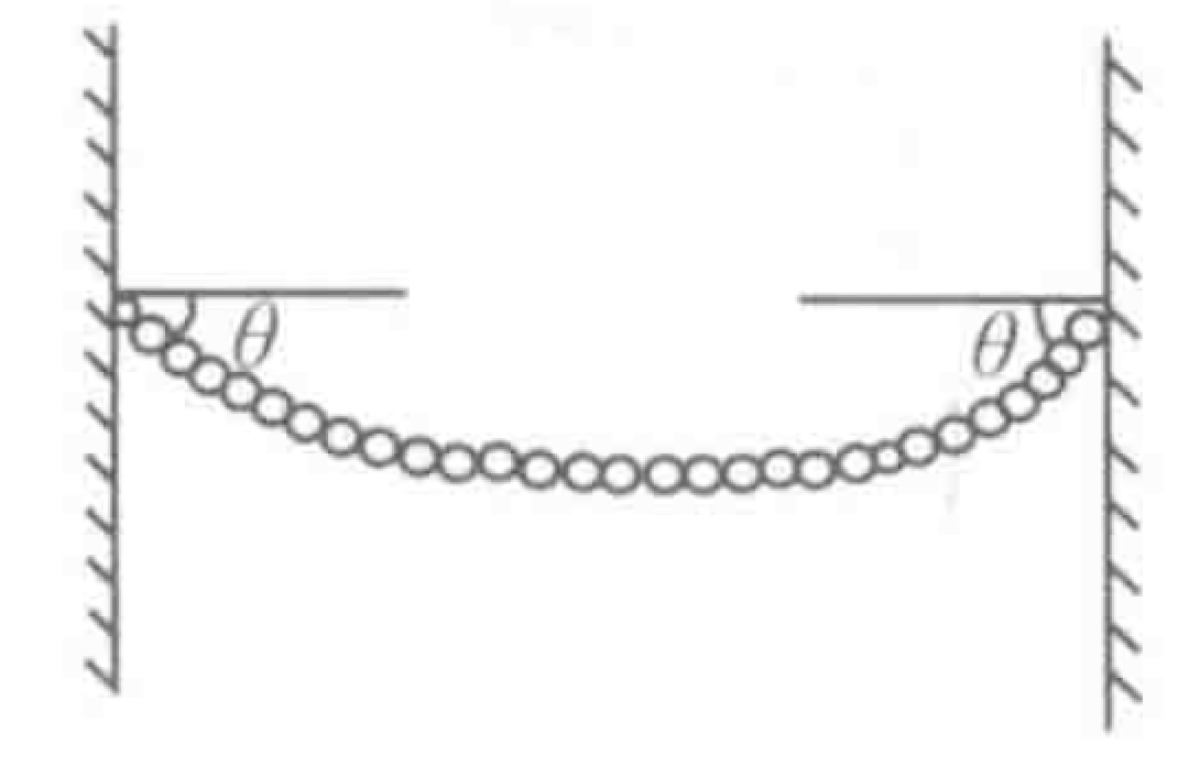
P0650-problem-1
[Q1] $F = \frac{G}{2 \sin\theta}$ [Q2] $T_{min} = \frac{G \cot\theta}{2}$
Let F be the force exerted by each hook on the chain. The system is in static equilibrium. For the entire chain, the vertical forces must balance. The total weight G is supported by the vertical components of the two end forces.
$$2 F \sin\theta = G$$ $$F = \frac{G}{2 \sin\theta}$$This answers the first question. For the second question, consider the right half of the chain. It is in equilibrium under three forces: the force F at the end, the weight of the half-chain ($G/2$), and the horizontal tension $T_{min}$ at the lowest point. For the horizontal forces on the half-chain to balance:
$$T_{min} = F \cos\theta$$Substituting the expression for F:
$$T_{min} = \left( \frac{G}{2 \sin\theta} \right) \cos\theta = \frac{G \cot\theta}{2}$$