Source: High school physics (Chinese)
Problem
In Figure 5.34, AOB is a pair of equal-arm tongs, with a frictionless pivot at O. A force is applied at A and B to grip a cylindrical object C. The weight of the cylindrical object is to be ignored.
- What factors determine whether the tongs can grip the cylinder?
- If the setup is just able to grip cylinder C (i.e., it is on the verge of slipping out), what condition must these factors satisfy?
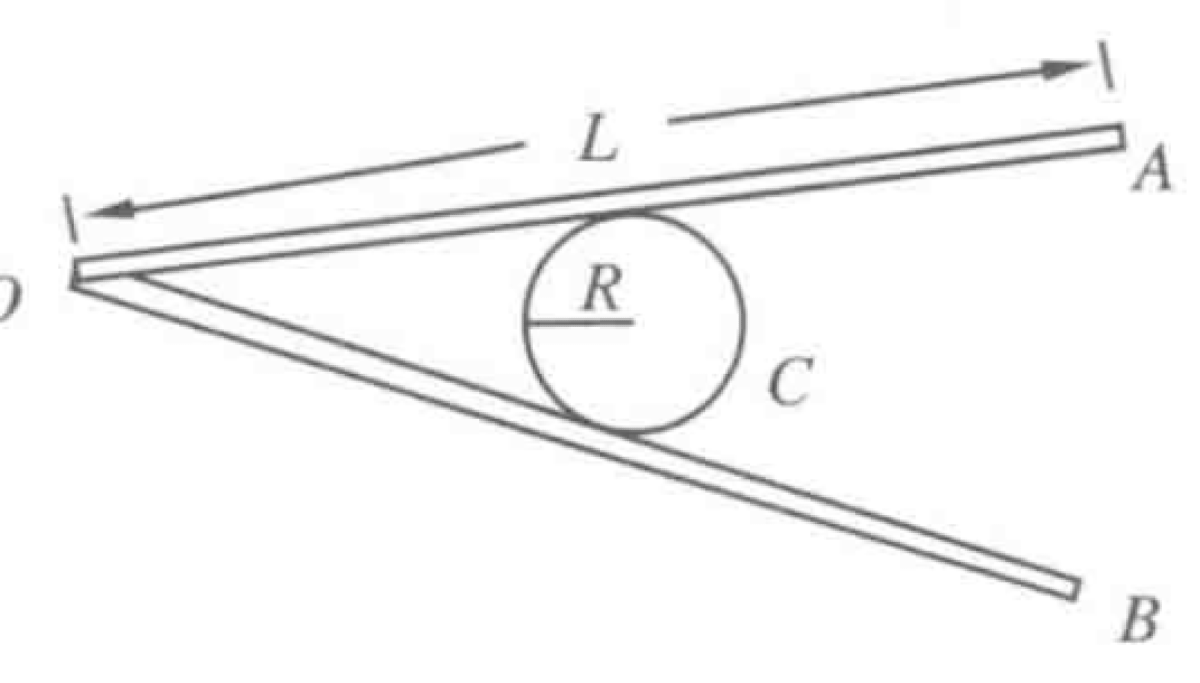
P0649-problem-1
[Q1] The factors are the coefficient of static friction ($\mu_s$) between the tongs and the cylinder, the radius of the cylinder ($R$), and the distance from the pivot to the point of contact ($x$). [Q2] The condition is $\mu_s = \tan\theta$, where $\theta$ is the half-angle between the tongs, or equivalently, $\mu_s = R/x$.
Let $2\theta$ be the angle between the tong arms OA and OB. Consider the forces acting on the cylinder C. Each arm exerts a normal force $N$ perpendicular to the arm and a static friction force $f_s$ parallel to the arm.
For the cylinder to be held, the outward-pushing component of the normal forces must be balanced by the inward-pulling component of the friction forces. Let the axis of symmetry be the x-axis (pointing away from the pivot). The total outward force from the two normal forces is $F_{out} = 2N \sin\theta$. The maximum inward force from static friction is $F_{in,max} = 2f_{s,max} \cos\theta = 2(\mu_s N) \cos\theta$, where $\mu_s$ is the coefficient of static friction.
To prevent the cylinder from slipping out, the condition $F_{out} \le F_{in,max}$ must be met.
$$2N \sin\theta \le 2\mu_s N \cos\theta$$Dividing by $2N \cos\theta$ gives the general condition for gripping:
$$\tan\theta \le \mu_s$$From the geometry, where $R$ is the cylinder's radius and $x$ is the distance from the pivot O to the point of contact, we have $\tan\theta = R/x$. Thus, the condition is $R/x \le \mu_s$.
The factors are the coefficient of static friction $\mu_s$, the cylinder radius $R$, and the contact position $x$. For the limiting case where the cylinder is about to slip, the equality holds.
$$\mu_s = \tan\theta = \frac{R}{x}$$