Source: High school physics (Chinese)
Problem
Two objects of mass $m_1$ and $m_2$ are connected by a string over a pulley as shown. Block $m_1$ hangs vertically, while block $m_2$ is on a horizontal surface with a coefficient of kinetic friction $\mu$. The pulley has a moment of inertia $I$ and a radius $r$. The string does not slip on the pulley.
- Find the acceleration $a$ of the system.
- Find the tensions $T_1$ and $T_2$ in the string.
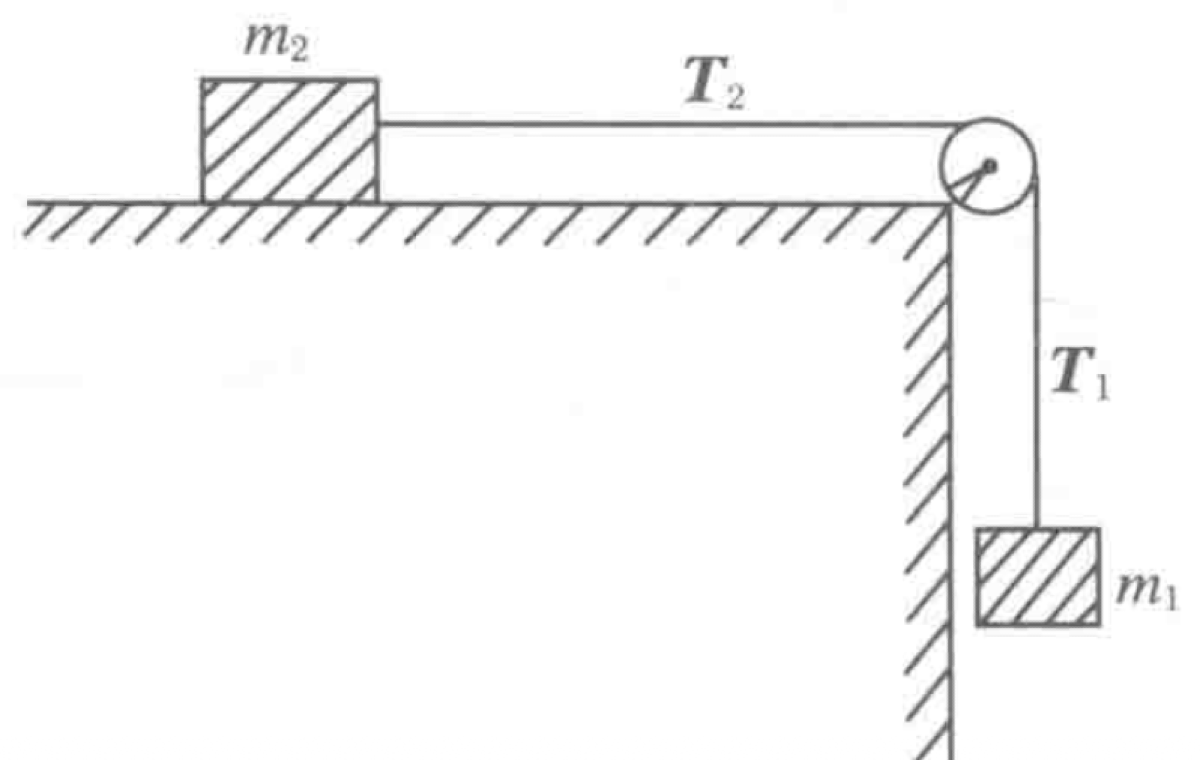
P0646-problem-1
Apply Newton's second law to each object and the pulley. Let the direction of motion (down for $m_1$, right for $m_2$) be positive.
For mass $m_1$:
$$m_1g - T_1 = m_1 a$$For mass $m_2$, the friction force is $f_k = \mu N = \mu m_2 g$:
$$T_2 - \mu m_2 g = m_2 a$$For the pulley, the net torque is $\tau = (T_1 - T_2)r$. Using $\tau = I\alpha$ and the no-slip condition $a = \alpha r$:
$$T_1 - T_2 = I \frac{a}{r^2}$$To solve for $a$, isolate $T_1$ and $T_2$ from the first two equations and substitute into the third:
$$(m_1g - m_1 a) - (m_2 a + \mu m_2 g) = \frac{I}{r^2} a$$Rearrange to solve for $a$:
$$m_1g - \mu m_2 g = a (m_1 + m_2 + \frac{I}{r^2})$$ $$a = \frac{(m_1 - \mu m_2)g}{m_1 + m_2 + I/r^2}$$Substitute $a$ back into the equations for $T_1$ and $T_2$:
$$T_1 = m_1(g - a)$$ $$T_2 = m_2(a + \mu g)$$