Source: High school physics (Chinese)
Problem Sets:
Problem
A uniform circular disk has a radius $R$. A circular hole with a radius of $R/2$ is cut from it, tangent to the center and the edge of the original disk.
- Find the distance of the center of mass of the remaining part from the center of the original disk.
- Find its moments of inertia about an axis at the center of the original disk and perpendicular to the disk
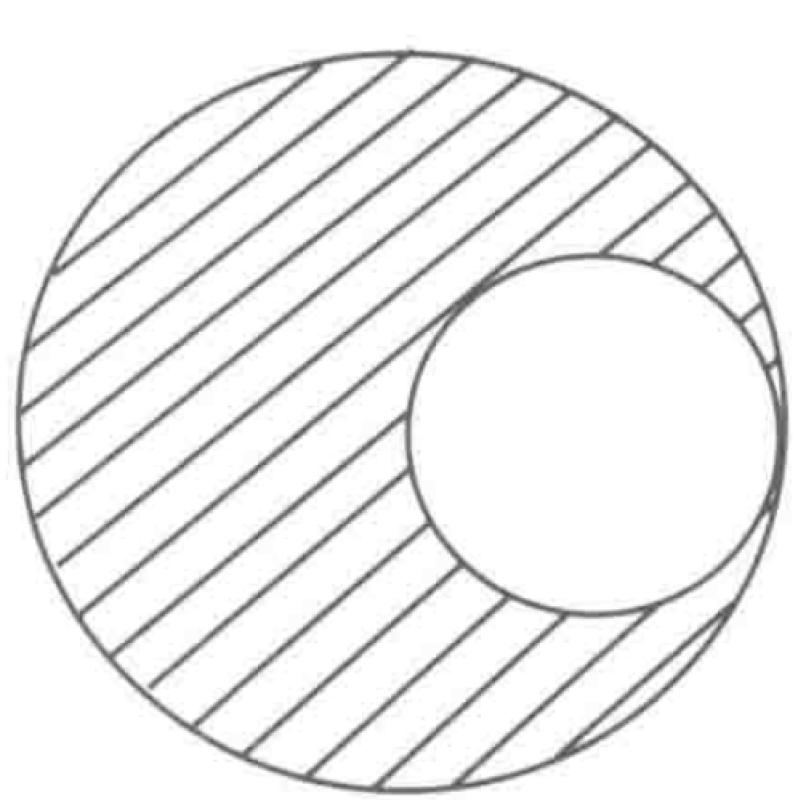
P0645-problem-1
[Q1] The distance of the center of mass from the center of the original disk is:
$$d_{CM} = \frac{R}{6}$$[Q2] The moment of inertia of the remaining part about the specified axis is:
$$I = \frac{13}{32}mR^2$$where $m$ is the mass of the original disk before the hole was cut.
This problem can be solved using the principle of superposition, treating the hole as an object with negative mass. Let $\sigma$ be the uniform surface mass density of the disk.
The original disk (object 1) has radius $R$ and mass $m_1 = \sigma \pi R^2$. Its center of mass is at the origin, $x_1=0$. The removed part (object 2, the hole) has radius $r=R/2$ and mass $m_2 = \sigma \pi (R/2)^2 = m_1/4$. Its center is located at $x_2=R/2$ (assuming the hole is on the positive x-axis). The remaining part (object 3) has mass $m_3 = m_1 - m_2 = m_1 - m_1/4 = \frac{3}{4}m_1$.
[Q1] Find the distance of the center of mass of the remaining part from the center of the original disk.
The center of mass of the composite system (original disk) is given by:
$$m_1 x_1 = m_2 x_2 + m_3 x_3$$We solve for the center of mass of the remaining part, $x_3 = x_{CM}$.
$$x_{CM} = \frac{m_1 x_1 - m_2 x_2}{m_3}$$Substituting the known values:
$$x_{CM} = \frac{m_1(0) - (m_1/4)(R/2)}{3m_1/4} = \frac{-m_1 R/8}{3m_1/4}$$ $$x_{CM} = -\frac{m_1 R}{8} \cdot \frac{4}{3m_1} = -\frac{R}{6}$$The negative sign indicates the center of mass shifts away from the hole. The distance from the original center is the magnitude of this value. Distance $= |x_{CM}| = \frac{R}{6}$
[Q2] Find its moments of inertia about an axis at the center of the original disk and perpendicular to the disk
The moment of inertia of the remaining part ($I_3$) can be found by subtracting the moment of inertia of the removed part ($I_2$) from that of the original disk ($I_1$), all calculated about the same axis (the center of the original disk, O).
$$I_3 = I_1 - I_2$$Let $m$ be the mass of the original disk, $m=m_1$. The moment of inertia of the original disk about its center O is:
$$I_1 = \frac{1}{2}mR^2$$To find the moment of inertia of the removed part ($I_2$) about O, we use the parallel axis theorem: $I = I_{cm} + md^2$. The center of mass of the hole is at a distance $d=R/2$ from O. The moment of inertia of the hole about its own center of mass is:
$$I_{2,cm} = \frac{1}{2}m_2 r^2 = \frac{1}{2}\left(\frac{m}{4}\right)\left(\frac{R}{2}\right)^2 = \frac{mR^2}{32}$$Applying the parallel axis theorem for the hole about O:
$$I_2 = I_{2,cm} + m_2 d^2 = \frac{mR^2}{32} + \left(\frac{m}{4}\right)\left(\frac{R}{2}\right)^2 = \frac{mR^2}{32} + \frac{mR^2}{16} = \frac{3mR^2}{32}$$Now, we find the moment of inertia of the remaining part:
$$I_3 = I_1 - I_2 = \frac{1}{2}mR^2 - \frac{3mR^2}{32} = \frac{16mR^2 - 3mR^2}{32} = \frac{13}{32}mR^2$$Here, $m$ is the mass of the original disk.