Source: High school physics (Chinese)
Problem
A flywheel with a mass of 60 kg and a diameter of 0.50 m rotates at 1000 rpm. It is brought to a stop in 5.0 s by a braking device as shown in Figure 5.25. The coefficient of friction between the brake shoe and the flywheel is 0.40. Assume the flywheel's mass is all distributed on its outer rim. Find the required braking force $F$. The lever pivots at the left end. The brake shoe is 0.50 m from the pivot, and the force $F$ is applied 1.25 m from the pivot.
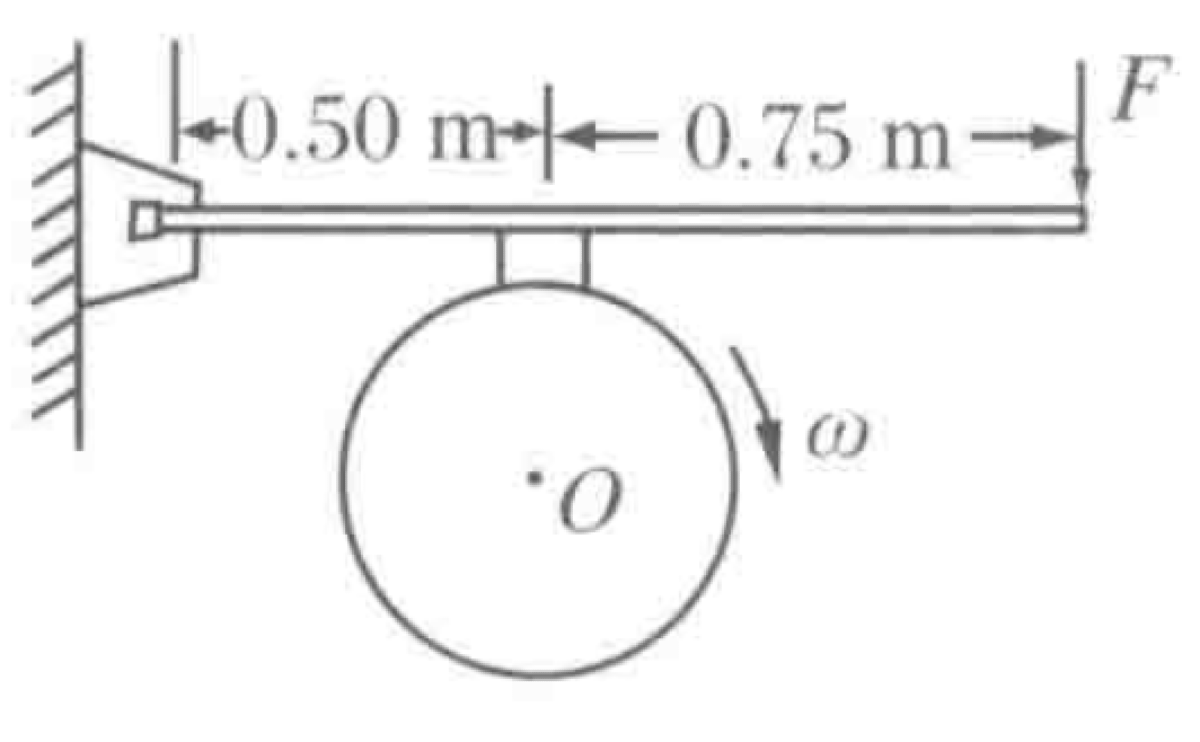
P0644-problem-1
This problem combines rotational dynamics with static equilibrium. First, we determine the angular deceleration required to stop the flywheel. Then, we calculate the braking torque needed. This torque is provided by friction, which allows us to find the normal force from the brake shoe. Finally, we use the static equilibrium of the lever to find the applied force $F$.
Initial angular velocity $\omega_0 = n_0 \frac{2\pi}{60}$. The required angular deceleration (magnitude) is $\alpha = \omega_0 / t$. The moment of inertia for a hoop is $I = MR^2$. The braking torque is $|\tau| = I\alpha$. This torque is produced by the friction force $f_k = \mu_k N$, so $|\tau| = f_k R = \mu_k N R$. This gives the required normal force $N$.
$$ N = \frac{|\tau|}{\mu_k R} = \frac{I\alpha}{\mu_k R} = \frac{(MR^2)(\omega_0/t)}{\mu_k R} = \frac{MR\omega_0}{\mu_k t} $$For the lever in equilibrium, the sum of torques about the pivot is zero: $F \cdot L_F - N \cdot L_N = 0$.
$$ F = N \frac{L_N}{L_F} = \left(\frac{MR\omega_0}{\mu_k t}\right) \frac{L_N}{L_F} = \left(\frac{MR(n_0 \frac{2\pi}{60})}{\mu_k t}\right) \frac{L_N}{L_F} $$Substituting the values: $M=60$ kg, $D=0.50$ m ($R=0.25$ m), $n_0 = 1000$ rpm, $t=5.0$ s, $\mu_k = 0.40$, $L_N=0.50$ m, $L_F=1.25$ m.
$$ \omega_0 = 1000 \frac{\text{rev}}{\text{min}} \left(\frac{2\pi \text{ rad}}{1 \text{ rev}}\right) \left(\frac{1 \text{ min}}{60 \text{ s}}\right) = \frac{100\pi}{3} \text{ rad/s} $$ $$ N = \frac{(60 \text{ kg})(0.25 \text{ m})(\frac{100\pi}{3} \text{ rad/s})}{(0.40)(5.0 \text{ s})} = 250\pi \text{ N} $$ $$ F = (250\pi \text{ N}) \frac{0.50 \text{ m}}{1.25 \text{ m}} = 100\pi \text{ N} \approx 3.1 \times 10^2 \text{ N} $$