Source: High school physics (Chinese)
Problem
Three uniform disks of the same material and thickness have radii $r_1=a$, $r_2=2a$, and $r_3=2a$. They are welded together in a line such that their edges touch, as shown in the diagram.
- Find the distance of the center of mass of the system from the center of the smallest disk (radius $a$).
- Find the moment of inertia around the center of the disk with radii $r_2=2a$.
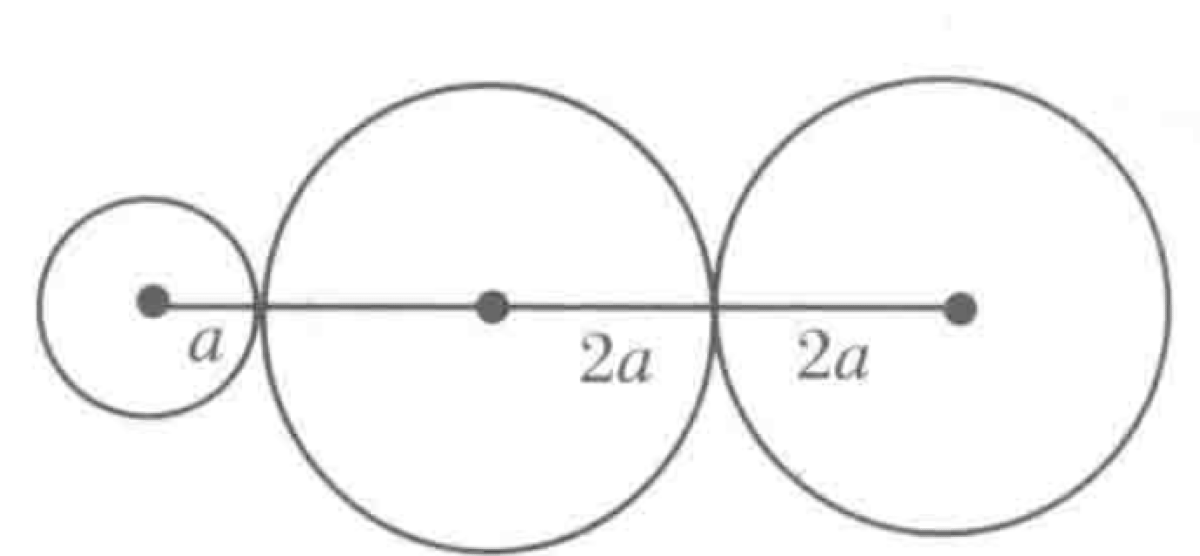
P0642-problem-1
[Q1] The distance of the center of mass from the center of the smallest disk is:
$$X_{CM} = \frac{40}{9}a$$[Q2] The moment of inertia around the center of the middle disk is:
$$I_{total} = \frac{179}{2}ma^2$$where $m$ is the mass of the smallest disk (radius $a$).
Let the three disks be indexed 1, 2, and 3 from left to right, with radii $r_1=a$, $r_2=2a$, and $r_3=2a$. Since they are made of the same uniform material and have the same thickness, their mass is proportional to their area, $m \propto r^2$. Let $m$ be the mass of the smallest disk (disk 1).
$$m_1 = m$$ $$m_2 = m \left(\frac{r_2}{r_1}\right)^2 = m \left(\frac{2a}{a}\right)^2 = 4m$$ $$m_3 = m \left(\frac{r_3}{r_1}\right)^2 = m \left(\frac{2a}{a}\right)^2 = 4m$$The total mass of the system is $M = m_1 + m_2 + m_3 = m + 4m + 4m = 9m$.
We set up a coordinate system with the origin at the center of the smallest disk (disk 1). The centers of the disks lie on the x-axis. The position of the center of disk 1 is $x_1 = 0$. The position of the center of disk 2 is $x_2 = r_1 + r_2 = a + 2a = 3a$. The position of the center of disk 3 is $x_3 = x_2 + (r_2 + r_3) = 3a + (2a + 2a) = 7a$.
[Q1] Find the distance of the center of mass of the system from the center of the smallest disk. The center of mass $X_{CM}$ is given by the formula:
$$X_{CM} = \frac{\sum m_i x_i}{\sum m_i} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{M}$$Substituting the values:
$$X_{CM} = \frac{m(0) + (4m)(3a) + (4m)(7a)}{9m} = \frac{0 + 12ma + 28ma}{9m}$$ $$X_{CM} = \frac{40ma}{9m} = \frac{40}{9}a$$[Q2] Find the moment of inertia around the center of the disk with radii $r_2=2a$. The total moment of inertia $I_{total}$ about an axis through the center of disk 2 is the sum of the moments of inertia of each disk about that axis. We use the parallel axis theorem, $I = I_{CM} + md^2$, where $I_{CM} = \frac{1}{2}mr^2$ for a disk. The axis of rotation is at $x=x_2=3a$.
Moment of inertia of disk 1 ($I_1$): The distance from the axis to the center of disk 1 is $d_1 = |x_2 - x_1| = 3a$.
$$I_1 = I_{CM,1} + m_1 d_1^2 = \frac{1}{2}m_1 r_1^2 + m_1 d_1^2 = \frac{1}{2}m a^2 + m(3a)^2 = \frac{1}{2}ma^2 + 9ma^2 = \frac{19}{2}ma^2$$Moment of inertia of disk 2 ($I_2$): The axis passes through its center, so $d_2=0$.
$$I_2 = I_{CM,2} = \frac{1}{2}m_2 r_2^2 = \frac{1}{2}(4m)(2a)^2 = \frac{1}{2}(4m)(4a^2) = 8ma^2$$Moment of inertia of disk 3 ($I_3$): The distance from the axis to the center of disk 3 is $d_3 = |x_3 - x_2| = 7a - 3a = 4a$.
$$I_3 = I_{CM,3} + m_3 d_3^2 = \frac{1}{2}m_3 r_3^2 + m_3 d_3^2 = \frac{1}{2}(4m)(2a)^2 + (4m)(4a)^2 = 8ma^2 + 64ma^2 = 72ma^2$$The total moment of inertia is the sum:
$$I_{total} = I_1 + I_2 + I_3 = \frac{19}{2}ma^2 + 8ma^2 + 72ma^2$$ $$I_{total} = \left(\frac{19}{2} + \frac{16}{2} + \frac{144}{2}\right)ma^2 = \frac{179}{2}ma^2$$