Source: High school physics (Chinese)
Problem
Two objects with masses $m_1 = 1.0$ kg and $m_2 = 2.0$ kg are placed at the ends of a light rod of length $l = 1.20$ m. The rod is supported by a fulcrum as shown in the figure. Take $g = 10$ m/s².
- How far from the 1.0 kg mass must the fulcrum be placed for the system to be in equilibrium?
- What is the force exerted on the fulcrum?
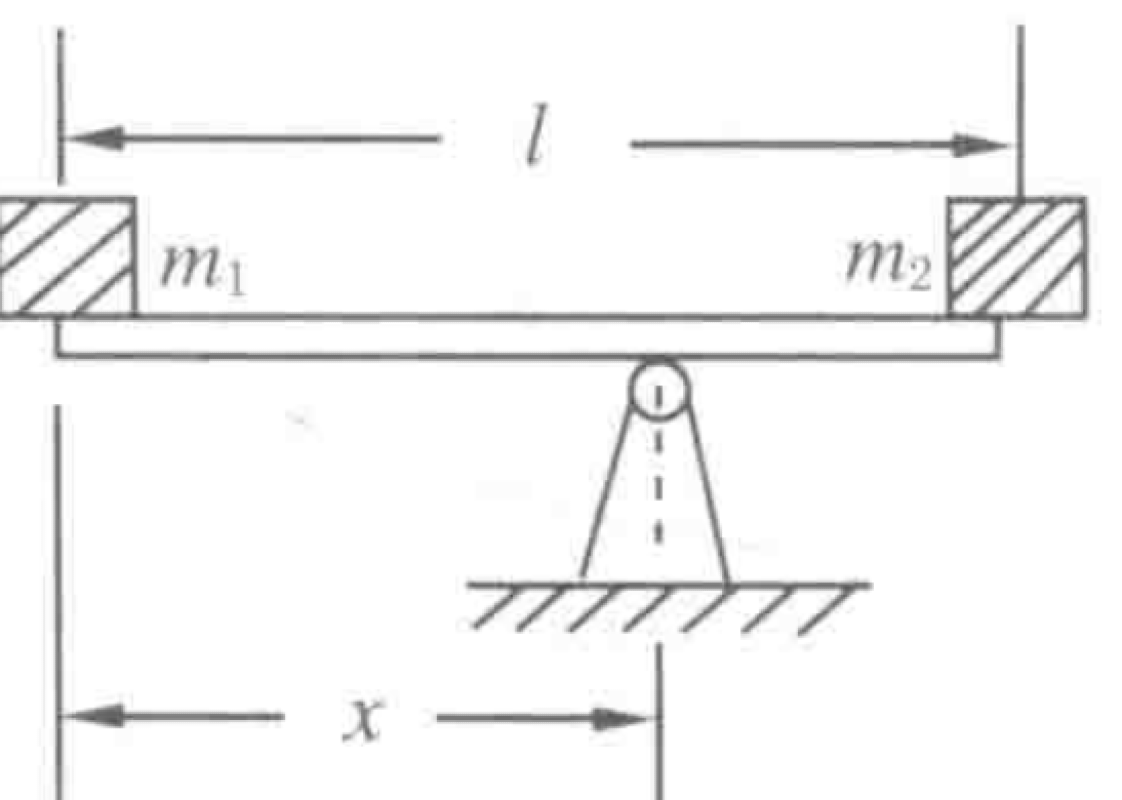
P0641-problem-1
[Q1] $x = 0.80$ m [Q2] $F_N = 30$ N
Let $x$ be the distance from mass $m_1$ to the fulcrum. For the rod to be in rotational equilibrium, the net torque about the fulcrum must be zero. The counter-clockwise torque from $m_1$ must balance the clockwise torque from $m_2$.
$$m_1 g x = m_2 g (l - x)$$Solving for $x$:
$$m_1 x = m_2 l - m_2 x$$ $$(m_1 + m_2) x = m_2 l$$ $$x = \frac{m_2 l}{m_1 + m_2}$$For the system to be in translational equilibrium, the net force must be zero. The upward support force from the fulcrum, $F_N$, must balance the total downward gravitational force.
$$F_N = m_1 g + m_2 g = (m_1 + m_2) g$$The force exerted on the fulcrum is equal in magnitude to $F_N$.