Source: High school physics (Chinese)
Problem Sets:
Problem
Two uniform rods are attached to a wall with hinges, and their other ends are joined by a bolt, as shown in the figure. The horizontal rod has a weight $W_1 = 120$ N and a length $L = 2.0$ m. The slanted rod has a weight $W_2 = 150$ N. The vertical distance between the two hinges on the wall is $h = 1.5$ m.
- Find the forces exerted by the hinges on the rods.
- Find the force exerted by the bolt on each rod.
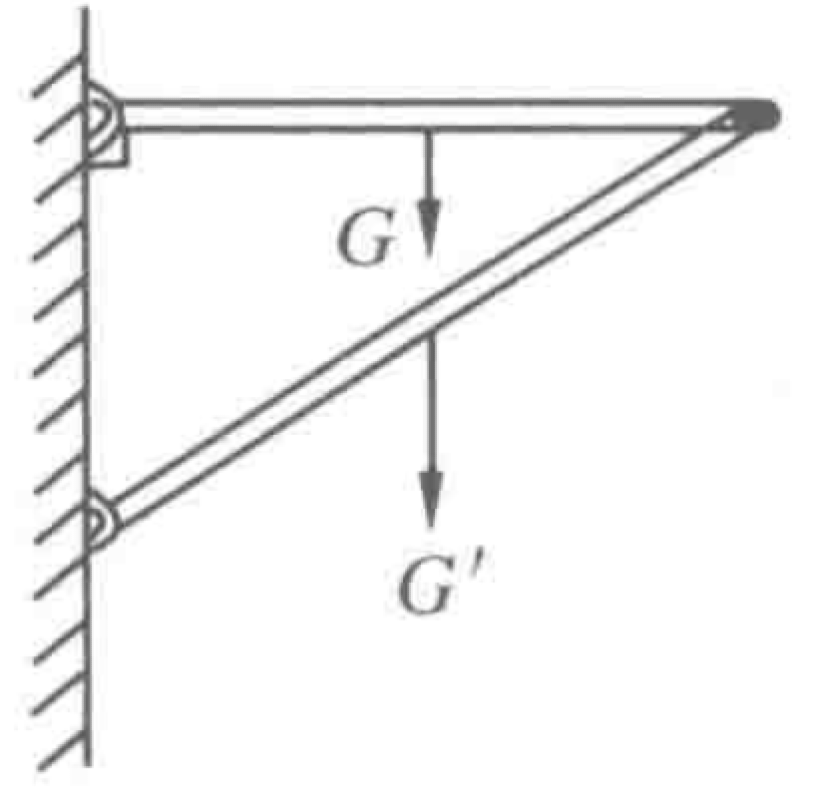
P0638-problem-1
[Q1] Force on upper hinge: $F_A = (-180, 60)$ N. Force on lower hinge: $F_B = (180, 210)$ N. [Q2] Force on horizontal rod: $F_{AC} = (180, 60)$ N. Force on slanted rod: $F_{BC} = (-180, -60)$ N.
Let A be the upper hinge, B be the lower hinge, and C be the bolt. Let the coordinate system originate at B, so B=(0,0), A=(0,h), and C=(L,h). Let $F_{AC}$ be the force exerted by the bolt on the horizontal rod AC, and $F_{BC}$ be the force on the slanted rod BC. By Newton's third law, $F_{AC} = -F_{BC}$. Let $F_{AC} = (F_x, F_y)$.
Consider the torque on the horizontal rod AC about hinge A:
$$\sum \tau_A = F_y L - W_1 \frac{L}{2} = 0$$ $$F_y = \frac{W_1}{2}$$Consider the torque on the slanted rod BC about hinge B. The force from the bolt is $(-F_x, -F_y)$ acting at C=(L,h). The weight $W_2$ acts at the rod's center, $(L/2, h/2)$.
$$\sum \tau_B = (L)(-F_y) - (h)(-F_x) - W_2 \frac{L}{2} = 0$$ $$-L F_y + h F_x - \frac{W_2 L}{2} = 0$$ $$F_x = \frac{L}{h} \left( F_y + \frac{W_2}{2} \right) = \frac{L}{h} \left( \frac{W_1}{2} + \frac{W_2}{2} \right) = \frac{L(W_1 + W_2)}{2h}$$The force from the hinge at A, $F_A = (A_x, A_y)$, is found from the equilibrium of rod AC:
$$A_x + F_x = 0 \implies A_x = -F_x$$ $$A_y - W_1 + F_y = 0 \implies A_y = W_1 - F_y$$The force from the hinge at B, $F_B = (B_x, B_y)$, is found from the equilibrium of rod BC:
$$B_x - F_x = 0 \implies B_x = F_x$$ $$B_y - W_2 - F_y = 0 \implies B_y = W_2 + F_y$$Substituting the given values:
$F_y = 120 / 2 = 60$ N $F_x = \frac{2.0(120 + 150)}{2(1.5)} = 180$ N $A_x = -180$ N $A_y = 120 - 60 = 60$ N $B_x = 180$ N $B_y = 150 + 60 = 210$ N