Source: High school physics (Chinese)
Problem Sets:
Problem
To roll a cylinder over an obstacle, it is known that the cylinder's radius is $R$, its weight is $G$, and the obstacle's height is $h$ (as shown in Figure).
- What horizontal force is needed if applied at the axle?
- What horizontal force is needed if applied at the highest point of the wheel?
- What is the minimum force required? What is its point of application and direction?
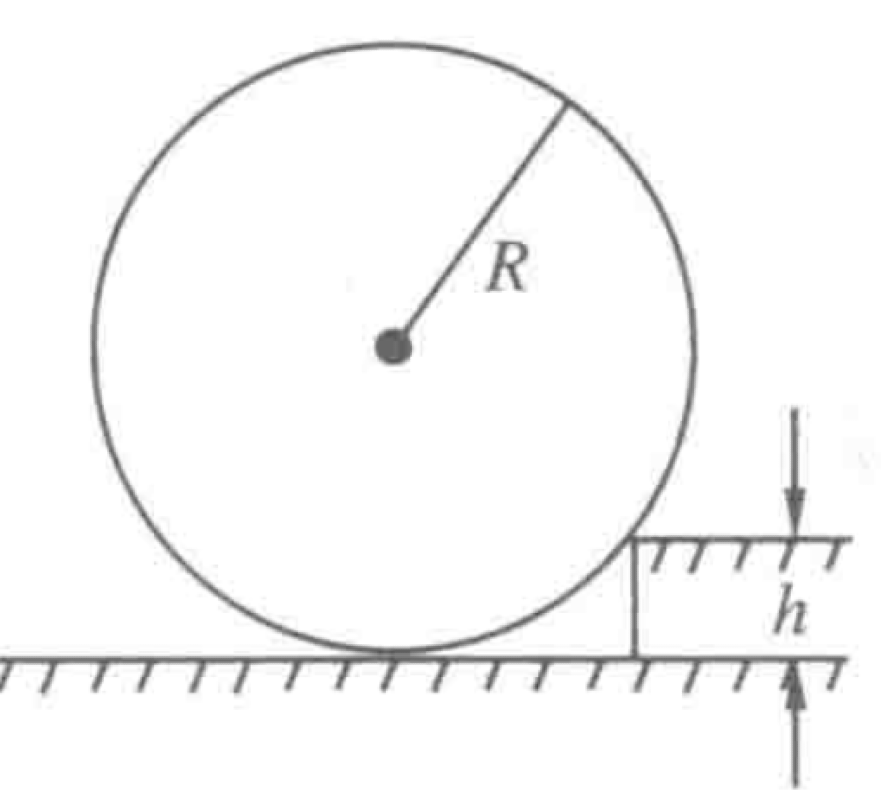
P0636-problem-1
[Q1] $F_1 = G \frac{\sqrt{2Rh-h^2}}{R-h}$ [Q2] $F_2 = G \frac{\sqrt{2Rh-h^2}}{2R-h}$ [Q3] $F_{min} = G \frac{\sqrt{2Rh-h^2}}{2R}$. The force is applied at the point on the circumference diametrically opposite the obstacle's corner, directed perpendicular to the diameter connecting these two points.
The cylinder pivots around the corner of the obstacle, P. To just lift the cylinder, the torque from the applied force ($\tau_F$) must balance the torque from gravity ($\tau_G$) about P. The lever arm for the weight $G$ is the horizontal distance from the center to the pivot, $d_G = \sqrt{R^2 - (R-h)^2} = \sqrt{2Rh-h^2}$. The torque due to gravity is $\tau_G = G d_G = G\sqrt{2Rh-h^2}$.
[Q1] A horizontal force $F_1$ is applied at the axle. The lever arm is the vertical distance from P to the axle, $d_1 = R-h$.
$$F_1 d_1 = \tau_G \implies F_1 (R-h) = G\sqrt{2Rh-h^2}$$ $$F_1 = G \frac{\sqrt{2Rh-h^2}}{R-h}$$[Q2] A horizontal force $F_2$ is applied at the highest point. The lever arm is $d_2 = (R-h) + R = 2R-h$.
$$F_2 d_2 = \tau_G \implies F_2 (2R-h) = G\sqrt{2Rh-h^2}$$ $$F_2 = G \frac{\sqrt{2Rh-h^2}}{2R-h}$$[Q3] To minimize the force $F_{min}$, the lever arm must be maximized. The maximum lever arm from the pivot P is the diameter of the wheel, $d_{max} = 2R$. This occurs when the force is applied at the point on the circumference diametrically opposite to P, and perpendicular to that diameter.
$$F_{min} d_{max} = \tau_G \implies F_{min} (2R) = G\sqrt{2Rh-h^2}$$ $$F_{min} = G \frac{\sqrt{2Rh-h^2}}{2R}$$The force is applied at the point on the rim diametrically opposite the corner of the step. Its direction is perpendicular to the line connecting this point and the pivot. This direction makes an angle $\theta$ with the horizontal, where $\cos\theta = \sqrt{2Rh-h^2}/R$.