Source: High school physics (Chinese)
Problem Sets:
Problem
A uniform rod AB, weighing $W_{rod} = 100$ N, has its center of gravity at its midpoint C. End A is connected to a wall by a hinge, allowing free rotation. End B is connected to the wall by a horizontal rope BE. The rod makes an angle of $60^\circ$ with the vertical wall, as shown in the diagram. An object weighing $W_{obj} = 300$ N is hung at point D, where the distance BD is one-third of the rod's length AB.
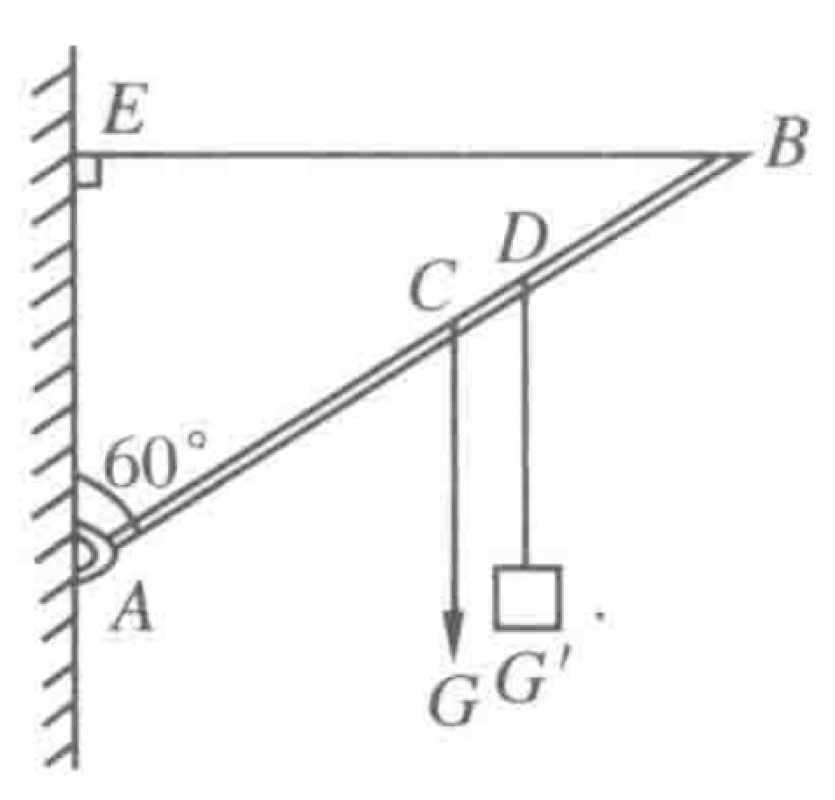
P0634-problem-1
The magnitude of the force is $F_A = 50\sqrt{139}$ N (approximately 589.5 N). The direction is $\phi = \arctan\left(\frac{8\sqrt{3}}{15}\right)$ (approximately $42.7^\circ$) above the horizontal.
Let the length of the rod be $L$. The angle the rod makes with the horizontal is $\theta = 90^\circ - 60^\circ = 30^\circ$. Let the tension in the rope be $T$, and the hinge reaction force have components $F_{Ax}$ and $F_{Ay}$. The rod is in static equilibrium, so the net torque and net force are zero.
Calculate the net torque about the hinge A:
$$\sum \tau_A = T(L \sin\theta) - W_{rod}(\frac{L}{2} \cos\theta) - W_{obj}((L-\frac{L}{3}) \cos\theta) = 0$$ $$T \sin\theta = (\frac{1}{2}W_{rod} + \frac{2}{3}W_{obj}) \cos\theta$$ $$T = (\frac{1}{2}W_{rod} + \frac{2}{3}W_{obj}) \cot\theta$$Substituting the values:
$$T = (\frac{1}{2}(100 \text{ N}) + \frac{2}{3}(300 \text{ N})) \cot(30^\circ) = (50 + 200)\sqrt{3} \text{ N} = 250\sqrt{3} \text{ N}$$Apply force equilibrium conditions:
$$\sum F_x = F_{Ax} - T = 0 \implies F_{Ax} = T = 250\sqrt{3} \text{ N}$$ $$\sum F_y = F_{Ay} - W_{rod} - W_{obj} = 0 \implies F_{Ay} = W_{rod} + W_{obj} = 100 \text{ N} + 300 \text{ N} = 400 \text{ N}$$The magnitude of the hinge force $F_A$ is:
$$F_A = \sqrt{F_{Ax}^2 + F_{Ay}^2} = \sqrt{(250\sqrt{3})^2 + 400^2} = \sqrt{187500 + 160000} = \sqrt{347500} = 50\sqrt{139} \text{ N}$$The direction of the hinge force, $\phi$, with respect to the horizontal is:
$$\phi = \arctan\left(\frac{F_{Ay}}{F_{Ax}}\right) = \arctan\left(\frac{400}{250\sqrt{3}}\right) = \arctan\left(\frac{8}{5\sqrt{3}}\right)$$