Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in Figure, the disk from the previous problem ($M=3.0$ kg, $R=0.15$ m) has a string wrapped around it. An object with weight $W=5.0$ N is hung from the string. The system is released from rest.
- What is the angular acceleration of the disk?
- What is the tangential acceleration of the disk's edge?
- What is the angular velocity of the disk at $t=2.0$ s?
- What is the velocity of the object at $t=2.0$ s?
- What is the rotational kinetic energy of the disk at $t=2.0$ s?
- What is the work done on the pulley by the tension in the string by $t=2.0$ s?
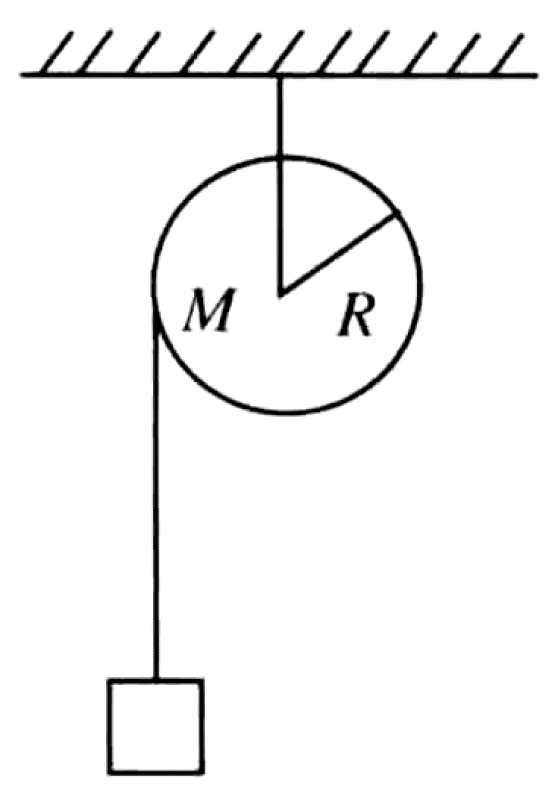
P0628-problem-1
[Q1] $\alpha = 16.6$ rad/s² [Q2] $a = 2.49$ m/s² [Q3] $\omega = 33.2$ rad/s [Q4] $v = 4.98$ m/s [Q5] $K_r = 18.6$ J [Q6] $W_T = 18.6$ J
Let $m$ be the hanging mass ($mg = W$) and $T$ be the tension. The system's linear acceleration is $a$ and angular acceleration is $\alpha$. Applying Newton's second law to the hanging mass:
$$mg - T = ma$$Applying Newton's second law for rotation to the disk ($I = \frac{1}{2}MR^2$):
$$\tau = TR = I\alpha$$The no-slip condition relates linear and angular acceleration: $a = \alpha R$. From the torque equation, we find the tension: $T = \frac{I\alpha}{R} = \frac{(\frac{1}{2}MR^2)(a/R)}{R} = \frac{1}{2}Ma$. Substitute $T$ into the first equation:
$$mg - \frac{1}{2}Ma = ma$$Solve for the acceleration $a$:
$$a = \frac{mg}{m + M/2} = \frac{W}{W/g + M/2}$$Use $g=9.8$ m/s². The remaining quantities are found using kinematics from rest ($\omega_0=0, v_0=0$):
$\alpha = a/R$, $\omega = \alpha t$, $v = at$, $K_r = \frac{1}{2}I\omega^2$.By the rotational work-energy theorem, the work done by the tension on the pulley, $W_T$, equals the change in the disk's rotational kinetic energy: $W_T = K_r$.