Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in Figure, a flywheel can rotate freely about a horizontal axis through its center O. A force of $F = 100$ N is applied at point P. The distance from the center is $OP = r = 50$ cm. The position vector $\vec{r} = \vec{OP}$ makes a 30° angle with the horizontal. The force $\vec{F}$, which is in the plane of the flywheel, makes a 45° angle with the horizontal.
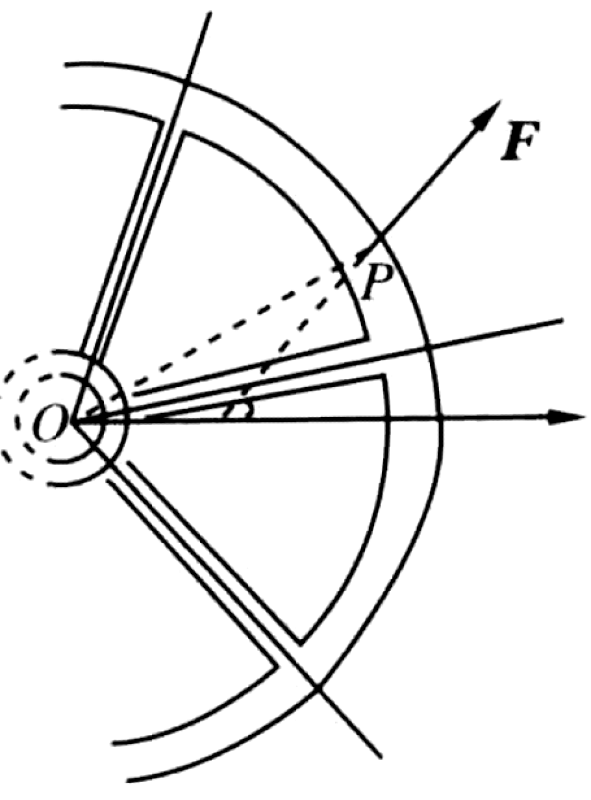
P0626-problem-1
The torque is given by the formula $\tau = rF\sin\theta$, where $\theta$ is the angle between the position vector $\vec{r}$ and the force vector $\vec{F}$. The angle between the two vectors is the difference between their angles with the horizontal.
$$\theta = 45^\circ - 30^\circ = 15^\circ$$The magnitude of the torque is:
$$\tau = rF\sin\theta$$Substituting the given values:
$$\tau = (0.50 \text{ m})(100 \text{ N})\sin(15^\circ)$$