Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in Figure, three rigid balls with masses $m_1$, $m_2=2m_1$, and $m_3=2m_1$ are placed in a horizontal, narrow, rigid circular groove fixed on a table. The balls are initially at positions I, II, and III, which are equidistant from each other. Friction is negligible. Initially, balls $m_2$ and $m_3$ are at rest, while ball $m_1$ moves along the groove with an initial velocity $v_0 = R\pi/2$, where $R$ is the effective radius of the groove. All collisions between the balls are perfectly elastic.
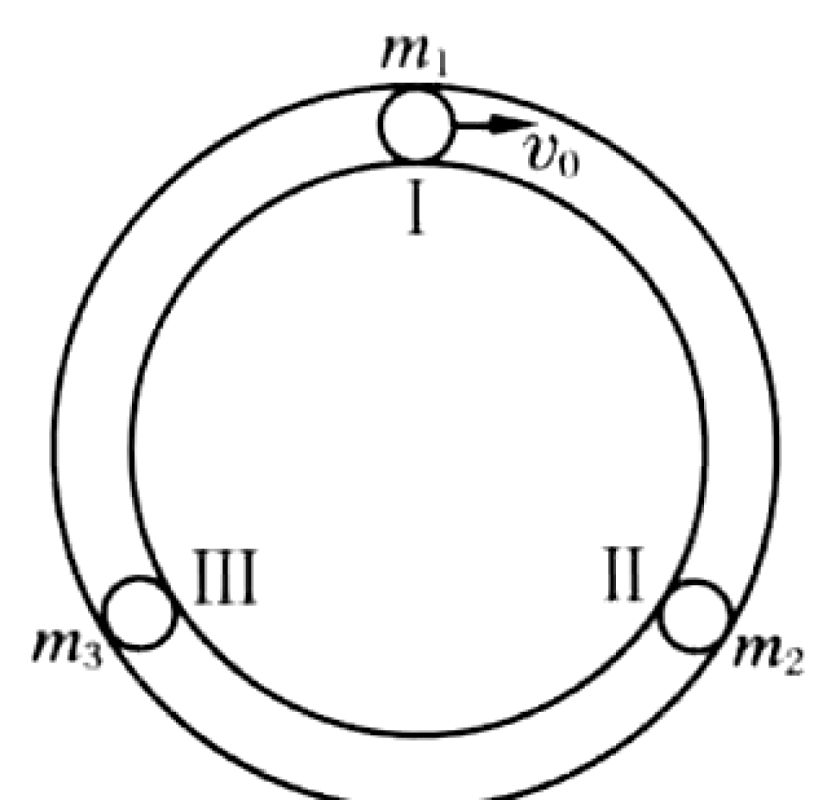
P0608-problem-1
[Q1] $T = 16/3$ s
The period $T$ is the time it takes for the system to return to a state where the velocity configuration repeats. The process involves a sequence of three elastic collisions.
-
Collision 1 ($m_1 \to m_2$): $m_1$ (velocity $v_0$) hits $m_2$ (at rest). Using conservation of momentum and kinetic energy for a 1D elastic collision, the final velocities $v_1'$ and $v_2'$ are:
$$v_1' = \frac{m_1-m_2}{m_1+m_2}v_0 = \frac{m_1-2m_1}{m_1+2m_1}v_0 = -\frac{1}{3}v_0$$ $$v_2' = \frac{2m_1}{m_1+m_2}v_0 = \frac{2m_1}{m_1+2m_1}v_0 = \frac{2}{3}v_0$$The time for this segment is $t_1 = \frac{2\pi R/3}{v_0} = \frac{2\pi R}{3v_0}$.
-
Collision 2 ($m_2 \to m_3$): $m_2$ (velocity $v_2'$) hits $m_3$ (at rest). Since $m_2=m_3$, they exchange velocities.
$$v_2'' = 0 \quad \text{and} \quad v_3' = v_2' = \frac{2}{3}v_0$$The time for this segment is $t_2 = \frac{2\pi R/3}{v_2'} = \frac{2\pi R/3}{2v_0/3} = \frac{\pi R}{v_0}$.
-
Collision 3 ($m_3 \to m_1$): $m_3$ (velocity $v_3'$) and $m_1$ (velocity $v_1'$) are moving towards each other. The arc length between them when collision 2 occurs is $\pi R$. The time until they collide is $t_3 = \frac{\pi R}{|v_1'| + |v_3'|} = \frac{\pi R}{v_0/3 + 2v_0/3} = \frac{\pi R}{v_0}$. After this collision, the velocities are $v_3''=0$ and $v_1''=v_0$. The system's velocity configuration $\{v_0, 0, 0\}$ is restored.
The period $T$ is the sum of the time intervals:
$$T = t_1 + t_2 + t_3 = \frac{2\pi R}{3v_0} + \frac{\pi R}{v_0} + \frac{\pi R}{v_0} = \frac{8\pi R}{3v_0}$$Given $v_0 = R\pi/2$:
$$T = \frac{8\pi R}{3(R\pi/2)} = \frac{16}{3} \text{s}$$