Source: High school physics (Chinese)
Problem Sets:
Problem
There are 5 small blocks (1, 2, 3, 4, 5), each with mass $m$ and negligible size. They are placed at equal distances $L$ on an inclined plane with an angle $\theta=30^\circ$. The incline is smooth above block 2 and rough below it. The coefficient of friction (static and kinetic) for all blocks on the rough section is $\mu$. Initially, block 1 is held at rest, while blocks 2, 3, 4, and 5 are at rest on the incline. Block 1 is then released, slides down, and collides with block 2. Subsequent collisions occur with the other blocks. All collisions are perfectly inelastic.
- For what range of values of $\mu$ will block 4 be hit, but block 5 will not be hit?
- What if the collision is elastic, for what range of values of $\mu$ will block 4 be hit, but block 5 will not be hit?
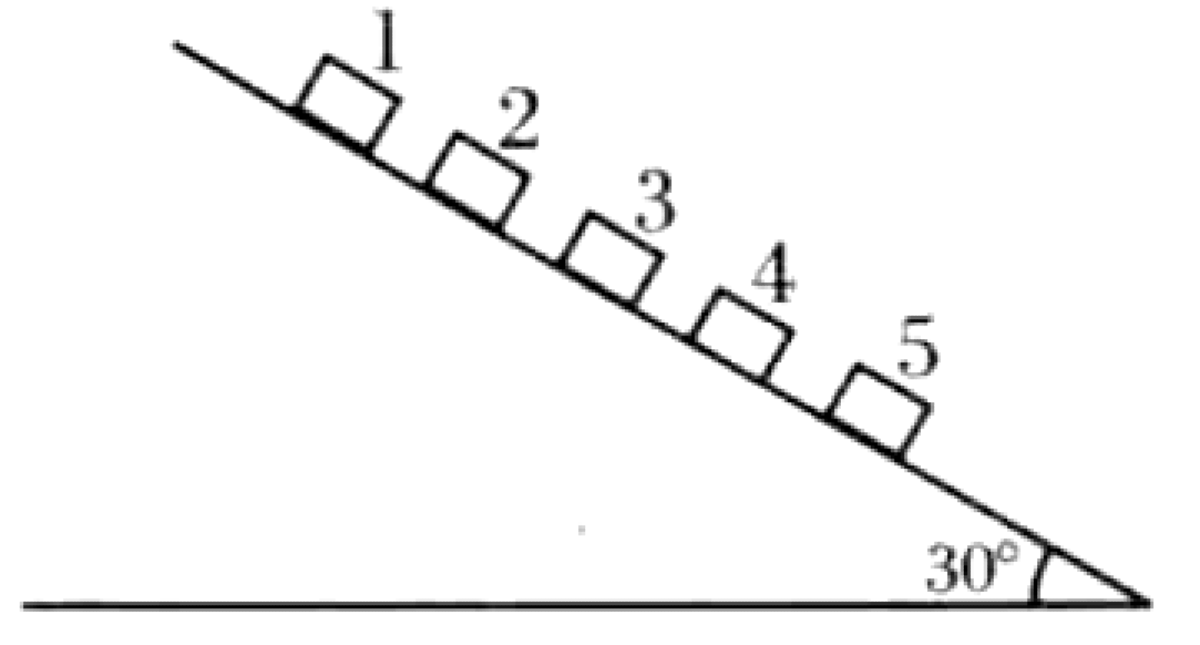
P0607-problem-1
Given $\theta=30^\circ$, so $\tan\theta = \frac{1}{\sqrt{3}}$.
[Q1] Perfectly Inelastic Collisions: The required range for $\mu$ is:
$$\frac{30}{29}\tan\theta \le \mu < \frac{14}{13}\tan\theta$$Substituting $\theta=30^\circ$:
$$\frac{30}{29\sqrt{3}} \le \mu < \frac{14}{13\sqrt{3}}$$[Q2] Elastic Collisions: The required range for $\mu$ is:
$$\frac{4}{3}\tan\theta \le \mu < \frac{3}{2}\tan\theta$$Substituting $\theta=30^\circ$:
$$\frac{4}{3\sqrt{3}} \le \mu < \frac{3}{2\sqrt{3}} \quad \text{or} \quad \frac{4\sqrt{3}}{9} \le \mu < \frac{\sqrt{3}}{2}$$[Q1] Perfectly Inelastic Collisions
We analyze the system using the work-energy theorem. Let $K_{k,f}$ be the kinetic energy of the combined mass of $k$ blocks just after the $(k-1)$-th collision, and $K_{k,i}$ be its kinetic energy just before the $k$-th collision (i.e., before hitting block $k+1$).
-
Motion of Block 1: Block 1 slides a distance $L$ on a smooth surface. Its kinetic energy just before hitting block 2 is:
$K_{1,i} = W_{gravity} = mgL\sin\theta$ -
Collision and Motion Recurrence Relations:
- Collision: For a perfectly inelastic collision where a moving mass $km$ (with kinetic energy $K_{k,i}$) hits a stationary mass $m$, the kinetic energy of the resulting mass $(k+1)m$ is found via momentum conservation. Let $v_{k,i}$ be the velocity of mass $km$. $K_{k,i} = \frac{1}{2}(km)v_{k,i}^2$. Momentum conservation: $(km)v_{k,i} = (k+1)m v_{k+1,f}$. The new kinetic energy is $K_{k+1,f} = \frac{1}{2}(k+1)m v_{k+1,f}^2 = \frac{1}{2}(k+1)m \left(\frac{k}{k+1}v_{k,i}\right)^2 = \frac{k^2}{k+1} \frac{1}{2}m v_{k,i}^2 = \frac{k}{k+1} \left(\frac{1}{2}km v_{k,i}^2\right) = \frac{k}{k+1} K_{k,i}$.
- Motion: Between collisions (from block $k$'s position to $(k+1)$'s), the combined mass $km$ moves a distance $L$ on a rough surface. The work done by the net force is $W_k = (kmg\sin\theta - \mu kmg\cos\theta)L$. By the work-energy theorem, the kinetic energy just before the next collision is: $K_{k,i} = K_{k,f} + W_k = K_{k,f} + kmgL(\sin\theta - \mu\cos\theta)$.
-
Step-by-Step Energy Calculation:
- After collision 1 (blocks 1+2): $K_{2,f} = \frac{1}{1+1} K_{1,i} = \frac{1}{2}mgL\sin\theta$.
- Before collision 2 (hitting block 3): $K_{2,i} = K_{2,f} + 2mgL(\sin\theta - \mu\cos\theta) = \frac{1}{2}mgL\sin\theta + 2mgL(\sin\theta - \mu\cos\theta) = mgL(\frac{5}{2}\sin\theta - 2\mu\cos\theta)$.
- After collision 2 (blocks 1+2+3): $K_{3,f} = \frac{2}{3}K_{2,i} = \frac{2}{3}mgL(\frac{5}{2}\sin\theta - 2\mu\cos\theta)$.
- Before collision 3 (hitting block 4): $K_{3,i} = K_{3,f} + 3mgL(\sin\theta - \mu\cos\theta) = \frac{2}{3}mgL(\frac{5}{2}\sin\theta - 2\mu\cos\theta) + 3mgL(\sin\theta - \mu\cos\theta)$ $K_{3,i} = mgL [(\frac{5}{3}+3)\sin\theta - (\frac{4}{3}+3)\mu\cos\theta] = \frac{mgL}{3}(14\sin\theta - 13\mu\cos\theta)$.
-
Condition 1: Block 4 is hit. The combined mass (1+2+3) must reach block 4, so its kinetic energy just before impact must be positive: $K_{3,i} > 0$.
$14\sin\theta - 13\mu\cos\theta > 0 \implies \mu < \frac{14}{13}\tan\theta$. -
Step-by-Step Energy Calculation (Continued):
- After collision 3 (blocks 1+2+3+4): $K_{4,f} = \frac{3}{4}K_{3,i} = \frac{3}{4}\frac{mgL}{3}(14\sin\theta - 13\mu\cos\theta) = \frac{mgL}{4}(14\sin\theta - 13\mu\cos\theta)$.
- Energy at block 5's position: The kinetic energy of mass $4m$ after traveling a distance $L$ towards block 5 would be: $K_{4,final} = K_{4,f} + 4mgL(\sin\theta - \mu\cos\theta) = \frac{mgL}{4}(14\sin\theta - 13\mu\cos\theta) + 4mgL(\sin\theta - \mu\cos\theta)$ $K_{4,final} = \frac{mgL}{4}[(14+16)\sin\theta - (13+16)\mu\cos\theta] = \frac{mgL}{4}(30\sin\theta - 29\mu\cos\theta)$.
-
Condition 2: Block 5 is not hit. The combined mass (1+2+3+4) must stop at or before reaching block 5. This means its kinetic energy at block 5's position is non-positive: $K_{4,final} \le 0$.
$30\sin\theta - 29\mu\cos\theta \le 0 \implies \mu \ge \frac{30}{29}\tan\theta$.
Combining both conditions, we find the range for $\mu$.
[Q2] Elastic Collisions
In a 1D elastic collision between two equal masses where one is at rest, they exchange velocities. The moving block stops, and the stationary block moves off with the incident velocity. This simplifies the problem to a sequence of single blocks moving one after another.
-
Energy Propagation: Let $K_k$ be the kinetic energy of block $k$ just as it starts moving, and $K'_k$ be its kinetic energy just before it hits block $k+1$.
- Block 1 starts on a smooth surface, so its energy before hitting block 2 is $K'_1 = mgL\sin\theta$.
- Due to velocity exchange, block 2 starts with this energy: $K_2 = K'_1 = mgL\sin\theta$.
- Block $k$ (for $k \ge 2$) moves on a rough surface. After traveling a distance $L$, its kinetic energy is: $K'_k = K_k + mgL(\sin\theta - \mu\cos\theta)$.
- Due to the next collision, $K_{k+1} = K'_k$. This leads to the recurrence relation: $K_{k+1} = K_k + mgL(\sin\theta - \mu\cos\theta)$.
This forms an arithmetic progression for the kinetic energy.
-
Step-by-Step Energy Calculation:
- $K_2 = mgL\sin\theta$.
- $K_3 = K_2 + mgL(\sin\theta - \mu\cos\theta) = mgL(2\sin\theta - \mu\cos\theta)$.
- $K_4 = K_3 + mgL(\sin\theta - \mu\cos\theta) = mgL(3\sin\theta - 2\mu\cos\theta)$.
-
Condition 1: Block 4 is hit. Block 3 must reach block 4, so its kinetic energy just before impact, $K'_3$, must be positive. Since $K_4 = K'_3$, this means $K_4 > 0$.
$3\sin\theta - 2\mu\cos\theta > 0 \implies \mu < \frac{3}{2}\tan\theta$. -
Step-by-Step Energy Calculation (Continued):
- The kinetic energy of block 4 just before hitting block 5 would be: $K'_4 = K_4 + mgL(\sin\theta - \mu\cos\theta) = mgL(3\sin\theta - 2\mu\cos\theta) + mgL(\sin\theta - \mu\cos\theta)$ $K'_4 = mgL(4\sin\theta - 3\mu\cos\theta)$.
-
Condition 2: Block 5 is not hit. Block 4 must stop at or before reaching block 5. Its kinetic energy at that point must be non-positive: $K'_4 \le 0$.
$4\sin\theta - 3\mu\cos\theta \le 0 \implies \mu \ge \frac{4}{3}\tan\theta$.
Combining both conditions, we find the range for $\mu$.