Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in the diagram, a light spring with spring constant $k$ connects objects A and B. The mass of object B is $m_B = m$, and the mass of object A is $m_A = 2m$. Another object C, with mass $m_C = m$, is placed in contact with object B. The entire system rests on a smooth horizontal surface. Initially, the system is held at rest with the spring compressed by 6 cm. The external forces are then removed.
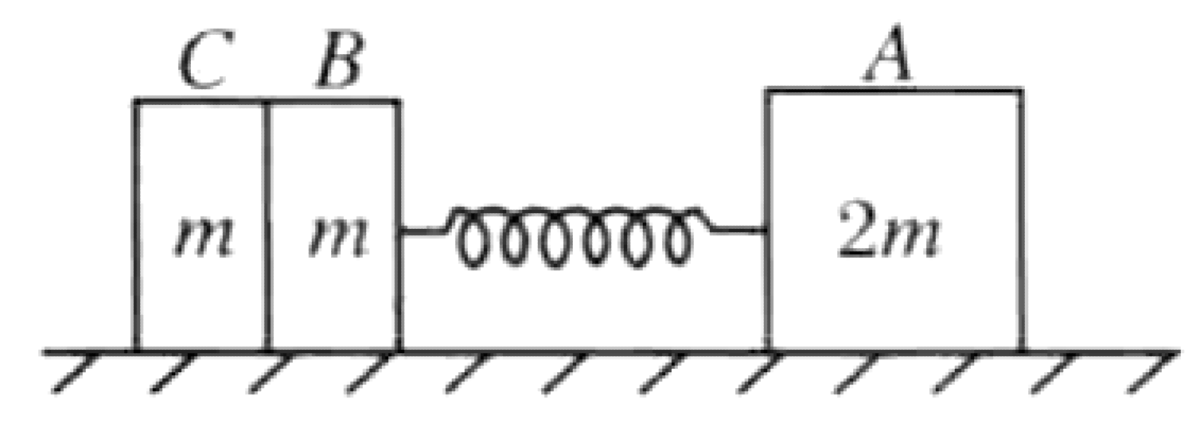
P0605-problem-1
The process is analyzed in two phases using conservation of momentum and energy.
Phase 1: From release until the spring reaches its natural length. The system consists of blocks A, B, and C. It starts from rest with initial spring potential energy $E_{p0} = \frac{1}{2}kx_0^2$, where $x_0 = 6$ cm is the initial compression. When the spring reaches its natural length, let the velocity of A be $v_A$ and the velocity of the combined block B+C be $v_{BC}$. By conservation of momentum (initial momentum is zero):
$$m_A v_A + (m_B+m_C)v_{BC} = 0$$ $$2mv_A + (m+m)v_{BC} = 0 \implies v_A = -v_{BC}$$Let $|v_A| = |v_{BC}| = v_1$. By conservation of energy:
$$E_{p0} = K_A + K_{BC}$$ $$\frac{1}{2}kx_0^2 = \frac{1}{2}m_A v_A^2 + \frac{1}{2}(m_B+m_C)v_{BC}^2 = \frac{1}{2}(2m)v_1^2 + \frac{1}{2}(2m)v_1^2 = 2mv_1^2$$Phase 2: From the spring's natural length to maximum extension. At the moment the spring reaches its natural length, block C separates from B, as the spring force on B becomes attractive. The system now consists of A and B. The initial velocities for this phase are $v_A = v_1$ and $v_B = v_{BC} = -v_1$. The total momentum of the A-B system is conserved: $P_{AB} = m_A v_A + m_B v_B = (2m)v_1 + m(-v_1) = mv_1$. The total energy of the A-B system is also conserved. At this moment, the energy is purely kinetic:
$$E_{AB} = \frac{1}{2}m_A v_A^2 + \frac{1}{2}m_B v_B^2 = \frac{1}{2}(2m)v_1^2 + \frac{1}{2}m(-v_1)^2 = \frac{3}{2}mv_1^2$$At maximum extension $x_{max}$, blocks A and B move with a common velocity $v_{com}$. By momentum conservation:
$$P_{AB} = (m_A+m_B)v_{com} \implies mv_1 = (2m+m)v_{com} \implies v_{com} = \frac{v_1}{3}$$The total energy at maximum extension is the sum of kinetic and potential energy:
$$E_{AB}' = \frac{1}{2}(m_A+m_B)v_{com}^2 + \frac{1}{2}kx_{max}^2 = \frac{1}{2}(3m)\left(\frac{v_1}{3}\right)^2 + \frac{1}{2}kx_{max}^2 = \frac{1}{6}mv_1^2 + \frac{1}{2}kx_{max}^2$$Equating the energies of the A-B system ($E_{AB}=E_{AB}'$):
$$\frac{3}{2}mv_1^2 = \frac{1}{6}mv_1^2 + \frac{1}{2}kx_{max}^2 \implies \frac{1}{2}kx_{max}^2 = \frac{4}{3}mv_1^2$$From Phase 1, we have $mv_1^2 = \frac{1}{4}kx_0^2$. Substituting this in:
$$\frac{1}{2}kx_{max}^2 = \frac{4}{3}\left(\frac{1}{4}kx_0^2\right) = \frac{1}{3}kx_0^2$$ $$x_{max}^2 = \frac{2}{3}x_0^2 \implies x_{max} = \sqrt{\frac{2}{3}}x_0$$Substituting $x_0 = 6$ cm:
$$x_{max} = \sqrt{\frac{2}{3}}(6 \text{ cm}) = \frac{\sqrt{6}}{3}(6 \text{ cm}) = 2\sqrt{6} \text{ cm}$$