Source: High school physics (Chinese)
Problem Sets:
Problem
Two children, A and B, are on sleds on frictionless ice. The mass of A plus sled is $M=30$ kg, and the mass of B plus sled is also $M=30$ kg. Child A, initially holding a box of mass $m=15$ kg, moves at $v_0=2.0$ m/s towards B, who is moving at the same speed $v_0$ towards A. To avoid a collision, A pushes the box towards B, and B catches it.
- What is the minimum speed (relative to the ground) the box must be pushed at to avoid a collision?
- How much work did A do on the box during the push?
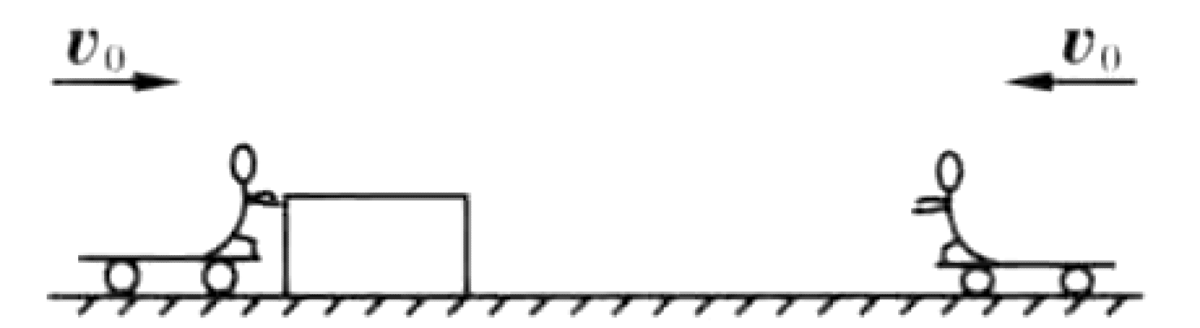
P0604-problem-1
[Q1] $v_{box} = 5.2$ m/s [Q2] $W_A = 172.8$ J
Let the initial direction of A be positive. [Q1] To just avoid a collision, the final velocity of A ($v_A$) must be equal to the final velocity of B with the box ($v_B$). Let this common velocity be $v_f$. The process can be analyzed in two steps, both conserving momentum.
- A pushes the box:
- B catches the box:
Set the condition $v_A = v_B = v_f$ and solve the system for $v_{box}$:
$$(M+m)v_0 = Mv_f + mv_{box} \quad (1)$$ $$mv_{box} - Mv_0 = (M+m)v_f \quad (2)$$From (2), $v_f = \frac{mv_{box} - Mv_0}{M+m}$. Substitute into (1):
$$(M+m)v_0 = M\left(\frac{mv_{box} - Mv_0}{M+m}\right) + mv_{box}$$ $$(M+m)^2 v_0 = Mmv_{box} - M^2 v_0 + m(M+m)v_{box}$$ $$(M^2+2Mm+m^2+M^2)v_0 = (Mm+Mm+m^2)v_{box}$$ $$(2M^2+2Mm+m^2)v_0 = (2Mm+m^2)v_{box}$$ $$v_{box} = \frac{2M^2+2Mm+m^2}{m(2M+m)}v_0$$Substituting values: $M=30$ kg, $m=15$ kg, $v_0=2.0$ m/s.
$$v_{box} = \frac{2(30)^2+2(30)(15)+15^2}{15(2 \cdot 30+15)}(2.0) = \frac{1800+900+225}{15(75)}(2.0) = \frac{2925}{1125}(2.0) = 5.2 \text{ m/s}$$[Q2] By the work-energy theorem, the work done by A on the box equals the change in the box's kinetic energy.
$$W_A = \Delta K_{box} = \frac{1}{2}m v_{box}^2 - \frac{1}{2}m v_0^2 = \frac{1}{2}m(v_{box}^2 - v_0^2)$$Substituting values:
$$W_A = \frac{1}{2}(15)(5.2^2 - 2.0^2) = 7.5(27.04-4.0) = 7.5(23.04) = 172.8 \text{ J}$$