Physics Arena

P0602 Mechanics › Momentum

Impulse on an Oscillating Mass

Momentum Intermediate Theorem of Momentum

Source: High school physics (Chinese)

Problem Sets:

momentum -1112

Problem

A spring is fixed at its upper end. An object A of mass m is attached to its lower end and hangs at equilibrium at position P. Another object B, also of mass m, is then hung from A by a thin string. After reaching a new equilibrium, the string is cut. Neglect spring mass and air resistance.

If object A has a speed v when it returns to position P, and at the same moment object B has a speed u, what is the magnitude of the impulse from the spring force on object A during this time interval?

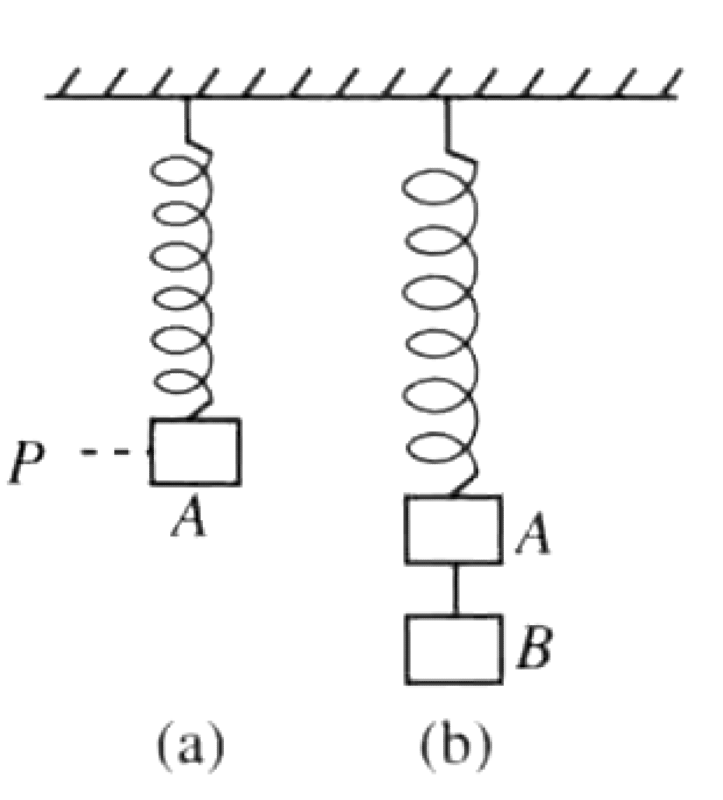
P0602-problem-1

$I_s = m(v+u)$

Apply the impulse-momentum theorem to object A. Let the upward direction be positive. The net impulse on A equals its change in momentum. The forces on A are the spring force $F_s$ and gravity $mg$. Let the time interval be $\Delta t$. The impulse from the spring force is $I_s$.

$$I_s - mg\Delta t = \Delta p_A = mv - 0$$

Object B is in free fall after the string is cut. Applying the impulse-momentum theorem to B, with the downward direction as positive:

$$mg\Delta t = \Delta p_B = mu - 0$$

From the equation for B, we find $mg\Delta t = mu$. Substitute this into the equation for A:

$$I_s = mv + mg\Delta t = mv + mu = m(v+u)$$