Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in the figure, a cart of mass $M$ has a smooth, quarter-circular track of radius $R$. A small block of mass $m$ slides down from the top of the track. The block and the cart are initially at rest. The friction on the wheels is negligible.
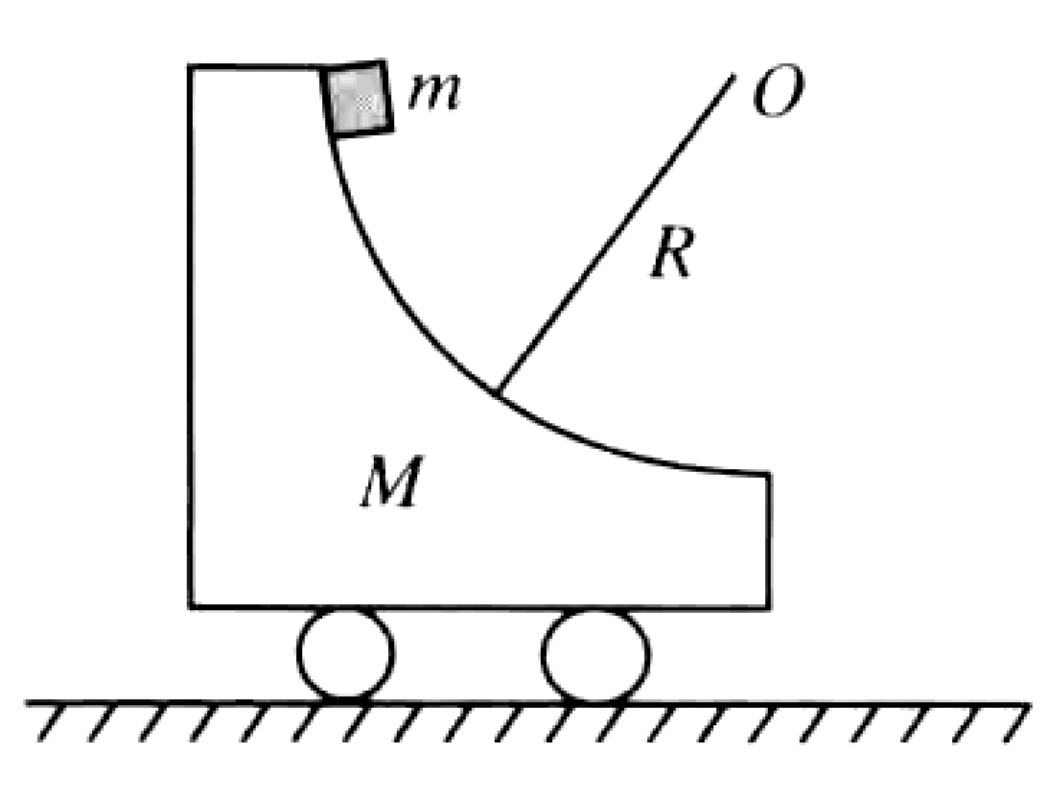
P0599-problem-1
Speed of the block: $v_m = \sqrt{\frac{2MgR}{M+m}}$ Speed of the cart: $V_M = \sqrt{\frac{2m^2gR}{M(M+m)}}$
The system consists of the block ($m$) and the cart ($M$). Since there are no external horizontal forces, the horizontal momentum of the system is conserved. As the track is smooth, the total mechanical energy is also conserved. Let $v_m$ and $v_M$ be the final speeds of the block and the cart relative to the ground.
Conservation of horizontal momentum (taking the direction of the block's final velocity as positive):
$$m v_m - M v_M = 0$$Conservation of mechanical energy (initial potential energy equals final kinetic energy):
$$mgR = \frac{1}{2}mv_m^2 + \frac{1}{2}MV_M^2$$From the momentum equation, $V_M = \frac{m}{M}v_m$. Substituting this into the energy equation:
$$mgR = \frac{1}{2}mv_m^2 + \frac{1}{2}M\left(\frac{m}{M}v_m\right)^2 = \frac{1}{2}mv_m^2\left(1 + \frac{m}{M}\right)$$Solving for $v_m$:
$$v_m^2 = \frac{2mgR}{m(1 + m/M)} = \frac{2MgR}{M+m} \implies v_m = \sqrt{\frac{2MgR}{M+m}}$$Then, solving for $V_M$:
$$V_M = \frac{m}{M}v_m = \frac{m}{M}\sqrt{\frac{2MgR}{M+m}} = \sqrt{\frac{2m^2gR}{M(M+m)}}$$