P0598 Mechanics › Momentum

Pendulum Collision and Coefficient of Restitution

← Back to Problems
Momentum Intermediate Collision

Source: High school physics (Chinese)

Problem Sets:

momentum - 1111

Problem

As shown in the figure, pendulum ball A is released from rest at an angle $\alpha = 45^\circ$. At the bottom of its swing, it collides head-on with the identical, stationary ball B. After the collision, ball B swings up to a maximum angle of $\beta = 30^\circ$. The masses of the balls are equal.

Find the coefficient of restitution for the collision (the ratio of relative speed after and before the collision).
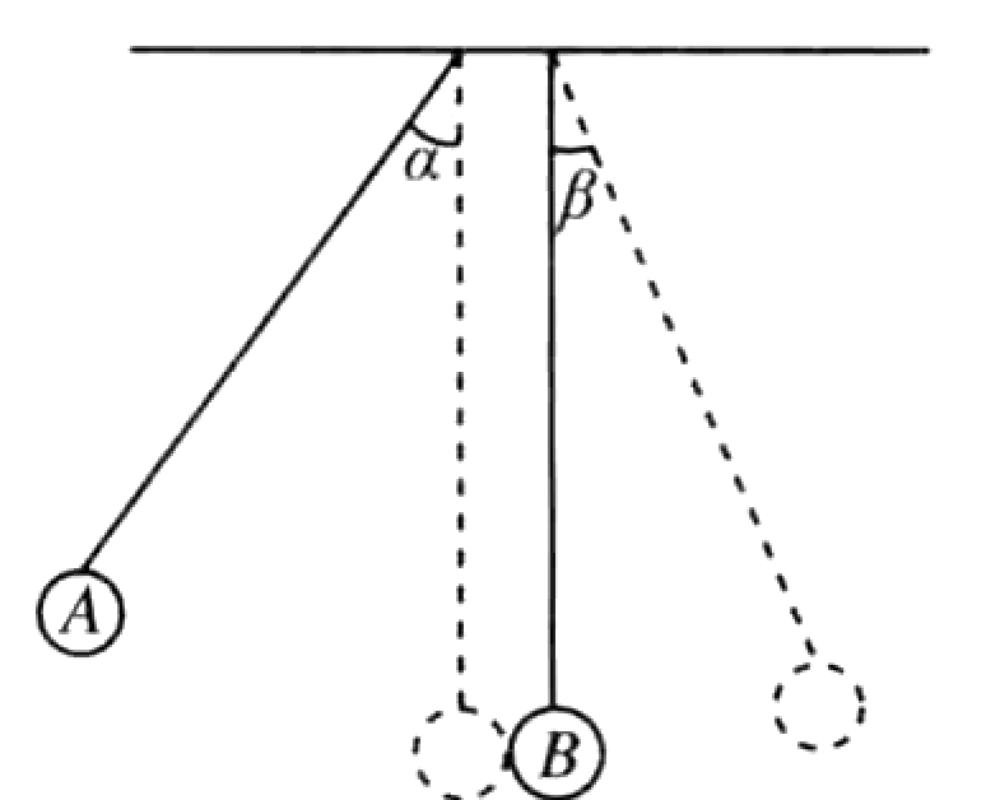
P0598-problem-1

P0598-problem-1

$e \approx 0.35$

Let the pendulum length be $L$ and the mass of each ball be $m$.

  1. Find the velocity of A just before collision, $v_A$, using conservation of energy:
$$m g L(1-\cos\alpha) = \frac{1}{2} m v_A^2 \implies v_A = \sqrt{2gL(1-\cos\alpha)}$$
  1. Find the velocity of B just after collision, $v_B'$, using conservation of energy:
$$\frac{1}{2} m (v_B')^2 = m g L(1-\cos\beta) \implies v_B' = \sqrt{2gL(1-\cos\beta)}$$
  1. Use conservation of momentum for the collision ($v_B=0, m_A=m_B=m$):
$$m v_A + 0 = m v_A' + m v_B' \implies v_A' = v_A - v_B'$$
  1. The coefficient of restitution $e$ is defined as:
$$e = \frac{v_B' - v_A'}{v_A - v_B} = \frac{v_B' - (v_A - v_B')}{v_A} = \frac{2v_B' - v_A}{v_A} = \frac{2v_B'}{v_A} - 1$$

Substituting the expressions for $v_A$ and $v_B'$:

$$e = 2 \frac{\sqrt{2gL(1-\cos\beta)}}{\sqrt{2gL(1-\cos\alpha)}} - 1 = 2\sqrt{\frac{1-\cos\beta}{1-\cos\alpha}} - 1$$ $$e = 2\sqrt{\frac{1-\cos(30^\circ)}{1-\cos(45^\circ)}} - 1 = 2\sqrt{\frac{1-\sqrt{3}/2}{1-\sqrt{2}/2}} - 1 \approx 0.35$$